để đa thức x3+3x2+5x+m chia hết cho đa thức x+3 thì giá trị m bằng mấy
Những câu hỏi liên quan
Tìm giá trị của m để đa thức x 3 + 3 x 2 - 5 x + m chia hết cho ( x - 2 )
để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán
Đúng 0
Bình luận (0)
Tìm m để đa thức A ( x ) = x 3 – 3 x 2 + 5 x + m chia hết cho đa thức B ( x ) = x – 2
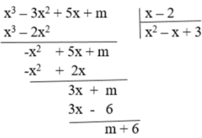
A(x) chia hết cho B(x) khi m + 6 = 0 ⇒ m= -6
Đúng 0
Bình luận (0)
tìm a để đa thức x3+3x2+5x+a chia hết cho đa thức x+3
\(\Leftrightarrow x^3+3x^2+5x+a=\left(x+3\right)\cdot a\left(x\right)\)
Thay \(x=-3\Leftrightarrow-27+27-15+a=0\Leftrightarrow a=15\)
Đúng 1
Bình luận (0)
Đặt \(x^3+3x^2+5x+a=f\left(x\right)\)
Gọi thương của đa thức \(f\left(x\right)\) là c(x)
⇒\(x^3+3x^2+5x+a=\left(x+3\right).c\left(x\right)\)
Tại x=-3 ⇒\(f\left(x\right)=-27+27-15+a=0\)
\(=a-15=0\)
⇒\(a=15\)
Đúng 2
Bình luận (0)
Cho đa thức f(x) =x3-3x2+3x-4.Với giá trị nguyên nào của x thì giá trị của đa thức f(x) chia hết cho giá trị của đa thức x2+2
x3-3x2+3x-4 x2+2
x3 +2x x-3
_____________
-3x2+x-4
-3x2 -6
_____________
x+2
-Để f(x) chia hết cho đa thức x2+2 thì:
\(x+2=0\Leftrightarrow x=2\)(nhận)
Đúng 0
Bình luận (0)
Cho đa thức A=x3 + 3x2 + 3x -2 và đa thức B= x+1
a) Thực hiện phép chia đa thức A cho đa thức B.
b) Tìm các giá trị nguyên của x để giá trị của đa thức A chia hết cho giá trị của đa thức B.
a: \(\dfrac{A}{B}=\dfrac{x^3+x^2+2x^2+2x+x+1-3}{x+1}=x^2+2x+1-\dfrac{3}{x+1}\)
b: Để A chia hết cho B thì \(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
Đúng 1
Bình luận (0)
Cho đa thức f(x)= x3+3x2+2x
a)phân tích các đa thức f(x) thành nhân tử
b) Tìm x để đa thức f(x)=0
c)tìm x nguyên để giá trị của đa thức f(x) chia hết cho x+3.
a. x3+x2+2x2+2x
= (x3+x2)+(2x2+2x)
= x2(x+1)+2x(x+1)
= (x2+2x)(x+1)
= x(x+2)(x+1)
Đúng 0
Bình luận (0)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2
Đúng 1
Bình luận (0)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)