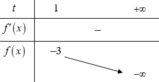
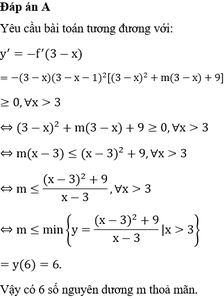Cho hàm số y=x^2-(m-2)x+m.Tìm m để HSĐB trên khoảng(2;+vô cực)

Những câu hỏi liên quan
Cho hàm số y = f(x) liên tục trên R sao cho maxf(x) = f(2) = bằng 84 trên [0; 10] . Xét hàm số g(x) = f(x3+x) - x2 + 2x + m.Tìm m để giá trị lớn nhất của g(x) trên [0; 2]
a. với giá trị nào của m thì hàm số y= ( m2 +4)x +3 là hsđb
b. với giá trị nào của m tì hàm số y= (m2 -2)x +31 là hsnb
c. chứng minh với mọi m, hàm số y=(m2+2m+2)x+3 luôn đồng biến trên R
a) (m^2+4)>0=> voi moi m
b)(m^2-2)<0=> -\(-\sqrt{2}< m< \sqrt{2}\)
c) (m^2+2m+2=(m+1)^2+1>0 voi m=>f(x) luon dong bien=> dpcm
Đúng 0
Bình luận (0)
tong quat y=ax+b
DB khi a>0
NB khi a<0
hang so khi a=0
giai
a. với giá trị nào của m thì hàm số y= ( m2 +4)x +3 là hsđb :
=> a>0=> m^2+4 >0 do m^2>=0=> m^2+4 >=0 tất nhiên >0 với mọi m
b. với giá trị nào của m tì hàm số y= (m2 -2)x +31 là hsnb
a<0=> m^2-2<0=> m^2<2=> !m!<\(\sqrt{2}=>-\sqrt{2}< m< \sqrt{2}\\ \)
c. chứng minh với mọi m, hàm số y=(m2+2m+2)x+3 luôn đồng biến trên R
ta ca
a=(m^2+2m+2=m^2+2m+1+1=(m+1)^2+1 do (m+1)^2>=0 moi m=> (m+1)^2+1>=1 voi moi m
=> a>0 với mọi m=> y luôn đồng biến
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
(
x
-
2
)
2
(
2
x
+
m
+
1
)
∀
x
∈
ℝ
Có bao nhiêu số nguyên âm m để hàm số
g
(
x
)
f
(
x...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 2 ) 2 ( 2 x + m + 1 ) ∀ x ∈ ℝ Có bao nhiêu số nguyên âm m để hàm số g ( x ) = f ( x 2 ) đồng biến trên khoảng
A. 5
B. 2
C. 3
D. 4
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
(
x
-
2
)
2
(
2
x
+
m
+
1
)
với mọi
x
∈
R
. Có bao nhiêu số nguyên âm m để hàm số
g
(
x
)
f
(
x...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 2 ) 2 ( 2 x + m + 1 ) với mọi x ∈ R . Có bao nhiêu số nguyên âm m để hàm số g ( x ) = f ( x 2 ) đồng biến trên khoảng ?
A. 5.
B. 2.
C. 3.
D. 4.
3. Cho hàm số y = x^2- m^2+2m +1 /x -m . Tìm tập hợp các giá trị của tham số m để hàm số đồng biến trên khoảng xác định của nó?
\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
1) hàm số \(y=\dfrac{x+5}{x+m}\) đồng biến trên khoảng (\(-\infty\),-8)
2) hàm số \(y=\dfrac{x+4}{x+m}\) đồng biến trên khoảng (\(-\infty\),-7)
3) hàm số \(y=\dfrac{x+2}{x+m}\) đồng biến trên khoảng (\(-\infty\),-5)
Cho hàm số yf(x) có đạo hàm f(x)
x
(
x
-
1
)
2
(
x
2
+
m
x
+
9
)
. Có bao nhiêu số nguyên dương m để hàm số yf(3-x) đồng biến trên khoảng
(
3
;
+
∞
)
. A. 6. B. 8. C. 5. D. 7.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Cho hàm số y = (2m+2)x + m -1. Tìm m để khoảng cách từ O đến đồ thị hàm số trên là lớn nhất.
Nếu \(2m+2=0\Rightarrow m=-1\Rightarrow y=-2\)
=> ĐTHS là đường thẳng đi qua (0;-2) và // với trục Ox
=> Khoảng cách từ O đến đths là 2
Nếu \(2m+2\ne0\Rightarrow m\ne-1\)
Khi đó ĐTHS \(y=\left(2m+2\right)x+m-1\) là đường thẳng đi qua điểm \(A\left(\frac{1-m}{2m+2};0\right)\) và \(B\left(0;m-1\right)\)
(ĐTHS bạn tự vẽ nhé)
Kẻ OH vuông góc với AB => OH là khoảng cách từ O đến đths
Tam giác AOB vuông tại O có OH là đường cao ứng với cạnh huyền nên ta có hệ thức sau:
\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{\left(\frac{1-m}{2m+2}\right)^2}+\frac{1}{\left(m-1\right)^2}=\frac{4m^2+8m+5}{m^2-2m+1}\)
\(\Rightarrow OH^2=\frac{m^2-2m+1}{4m^2+8m+5}\)
Đặt \(OH^2=a\ge0\)
\(\Rightarrow4m^2a+8ma+5a=m^2-2m+1\)
\(\Leftrightarrow m^2\left(4a-1\right)+2m\left(4a+1\right)+\left(5a-1\right)=0\)
\(\Delta^'=\left(4a+1\right)^2-\left(4a-1\right)\left(5a-1\right)=16a^2+8a+1-20a^2+9a-1\)
\(=-4a^2+17a=-a\left(4a-17\right)\)
\(\Delta^'\ge0\Leftrightarrow a\left(4a-17\right)\le0\Rightarrow0\le a\le\frac{17}{4}\)
\(\Rightarrow a_{max}=\frac{17}{4}\Rightarrow OH^2=\frac{17}{4}\Rightarrow OH=\frac{\sqrt{17}}{2}\)
Dấu "=" xảy ra khi: \(\frac{m^2-2m+1}{4m^2+8m+5}=\frac{17}{4}\Leftrightarrow4m^2-8m+4=68m^2+136m+85\)
\(\Leftrightarrow64m^2+144m+81=0\Leftrightarrow\left(8m+9\right)^2=0\Rightarrow m=-\frac{9}{8}\)
Vậy khoảng cách lớn nhất từ O đến đths là \(\frac{\sqrt{17}}{2}\) khi \(m=-\frac{9}{8}\)
Cho hàm số y f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sauCó bao nhiêu giá trị nguyên của tham số m để hàm số g (x) f (x + m) đồng biến trên khoảng (0; 2). A. 3 B. 4 C. 2 D. 1
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).
A. 3
B. 4
C. 2
D. 1