Cho ΔABC có góc A =60*, góc B=45*, b=8.
a) Tính a,c, góc C
b) Tính diện tích tam giác
* Cho ΔABC có BC=12cm, góc B=\(60^0\), góc C=\(40^0\)
a. Tính đường cao CH và cạnh AC
b. Tính diện tích ΔABC (làm tròn đến chữ số thập phân thứ 2)
* Cho ΔABC vuông tại A có góc B= \(30^0\), AB=6cm
a. Giải tam giác vuông ABC
b. Vẽ đường cao AH, trung tuyến AM của ΔABC. Tính diện tích ΔAHM
1.
\(a,\sin\widehat{B}=\sin60^0=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}\Leftrightarrow AC=\dfrac{12\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\\ b,AC^2=CH\cdot BC\left(HTL.\Delta\right)\\ \Rightarrow CH=\dfrac{AC^2}{BC}=9\left(cm\right)\)
Tim Gia Tri Nho Nhat Cua
a) A = x - 4 can x + 9
b) B = x - 3 can x - 10
c ) C = x - can x + 1
d ) D = x + can x + 2
Bài 2:
a: Xét ΔABC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\Leftrightarrow BC=6:\sin60^0=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
1. Tam giác ABC vuông góc tại A, đường cao AH. Biết AB:AC=3:4. Và AB+AC=21
a. Tính độ dài các cạnh tam giác ABC
b. Tính độ dài các đoạn AH, BH, CH
2. Cho hình thang ABCD có góc A=góc D= 90 độ; góc B= 60 độ; CD=30 cm; CA vuông góc với CB. Tính diện tích hình thang
1. Tam giác ABC vuông góc tại A, đường cao AH. Biết AB:AC=3:4. Và AB+AC=21
a. Tính độ dài các cạnh tam giác ABC
b. Tính độ dài các đoạn AH, BH, CH
2. Cho hình thang ABCD có góc A=góc D= 90 độ; góc B= 60 độ; CD=30 cm; CA vuông góc với CB. Tính diện tích hình thang
AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm
Cho ΔABC có 3 góc đều nhọn, hai đường cao BD và CE.
a) Chứng minh ΔADB ~ ΔAEC
b) Chứng minh ΔAED ~ ΔACB
c) Cho góc A của ΔABC bằng 60o và diện tích tam giác ABC bằng 120cm ². Tính diện tích của ΔADE
* Cho ΔABC vuông tại A có B= \(30^0\), AB=6cm
a. Giải ΔABC
b. Vẽ đường cao AH và trung tuyến AM của ΔABC. Tính diện tích ΔAHM
* Cho ΔABC vuông tại A có AB=3 cm, BC=5cm, đường cao AH
a. Tính số đo góc B, C
b. Gọi AE là phân giác của góc A (E ∈ BC). Tính AE
Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
Cho tam giác ABC có
a) AB=16cm BC=14cm góc b=60•.Tính các cạnh các góc còn lại và tính diện tích tam giác ABC
b) AB=16cm BC=14cm CA=24cm.Tính các góc và tính diện tích tam giác ABC
c) góc a=50• AB=20cm góc b=60•.Tính các cạnh các góc còn lại và tính diện tích tam giác ABC
Bạn kể thêm đường cao và đặt ẩn là làm ra
1 ) Cho tam giác ABC có góc A nhọn , AB=4 , AC=5 và diện tích tam giác ABC =8 . Tính BC
2 ) Cho tam giác ABC có AB=3 , góc ACB = 45° , góc ABC = 60° . Tính BC
em mới học lớp 7 hà
năm nay lên lớp 8 =)))))
1)Ta có: \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
\(\Leftrightarrow8=\dfrac{1}{2}\times4\times5\times sinA\)
\(\Leftrightarrow\sin A=0,8\)
Lại có: \(\left(\sin A\right)^2+\left(\cos A\right)^2=1\Leftrightarrow\cos A=0,6.\)
Áp dụng định lí hàm số cosin:
\(BC^2=AB^2+AC^2-2AB\times AC\times\cos A\)
\(\Leftrightarrow BC^2=4^2+5^2-2\times4\times5\times0,6=17\)
\(\Leftrightarrow BC=\sqrt{17}.\)
2) Trong \(\Delta ABC\) có: \(g\text{ó}cA+g\text{óc}B+g\text{óc}C=180^o\)
=> BAC=75o.
Áp dụng định lí hàm số sin:
\(\dfrac{AB}{\sin C}=\dfrac{BC}{\sin A}\Leftrightarrow\dfrac{3}{\sin45^o}=\dfrac{BC}{\sin75^o}\)
\(\Leftrightarrow BC=\dfrac{3+3\sqrt{3}}{2}\).
Cho hình lăng trụ ABC A'B'C' có AA'=a, góc giữa cạnh bên và mặt đáy bằng 60°. Tam giác ABC vuông tại C và góc B A C ^ = 60 ° . Hình chiếu vuông góc của B' lên mặt phẳng A B C trùng với trọng tâm của Δ A B C . Tính thể tích khối tứ diện A'ABC theo a
A. V A ' A B C = 3 a 3 208
B. V A ' A B C = 27 a 3 208
C. V A ' A B C = 81 a 3 208
D. V A ' A B C = 9 a 3 208
Đáp án D.
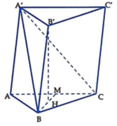
Gọi H là trọng tâm của tam giác ABC, từ giả thiết suy ra B ' H ⊥ A B C .
Khi đó
B B ' , A B C ^ = B B ' , B H ^ = B ' B H ^ = 60 °
Ta có
B B ' = a ⇒ B H = B B ' . cos B ' B H ^ = a . cos 60 ° = a 2 , B ' H = B ' B 2 − B H 2 = a 3 2
Gọi M là trung điểm BC, suy ra B H = 2 3 B M ⇒ B M = 3 2 B H = 3 2 . a 2 = 3 a 4 .
Đặt A C = x > 0 ⇒ B C = A C . tan B A C ^ = x . tan 60 ° = x 3 ⇒ A B = A B 2 + A C 2 = 2 x .
Lại có
B M = B C 2 + C M 2 = B C 2 + A C 2 4 = 3 x 2 + x 2 4 = x 13 2 = 3 a 4 ⇒ x = 3 a 2 13
⇒ A C = 3 a 2 13 , B C = 3 3 a 2 13 , A B = 6 a 2 13 ⇒ S Δ A B C = 1 2 A C . B C = 9 3 a 2 104
(đvdt).
Vậy V A ' A B C = 1 3 B ' H . S Δ A B C = 1 3 . a 3 2 . 9 3 a 2 104 = 9 a 3 208 (đvtt).
Cho tam giác ABC có góc A=60° C=45° R=5 tính diện tích tam giác ABC
\(\widehat{B}=180^o-60^o-45^o=75^o\)
Theo định lý sin ta có:
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=\dfrac{AB\cdot sinB}{sinC}=\dfrac{5\cdot sin75^o}{sin45^o}=\dfrac{5+5\sqrt{3}}{2}\)
Mà: \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot5\cdot\dfrac{5+5\sqrt{3}}{2}\cdot sin60^o=\dfrac{75+25\sqrt{3}}{8}\left(dvdt\right)\)
cho tam giác abc, góc A=90°, góc B =60°, AB=8cm a) tính góc C, cạnh Ac và BC b) tính diện tích tam giác ABC
Ta có \(\widehat{A}=90^0\Rightarrow\Delta ABC\) vuông tại \(A\)
\(a,\widehat{C}=90^0-\widehat{B}=30^0\\ AC=\tan B\cdot AB=\tan60^0\cdot8=8\sqrt{3}\left(cm\right)\\ BC=\dfrac{AB}{\sin C}=\dfrac{8}{\sin30^0}=16\left(cm\right)\\ b,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot8\cdot8\sqrt{3}=32\sqrt{3}\left(cm^2\right)\)