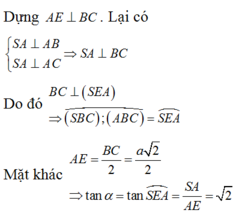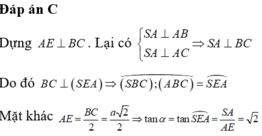Cho tứ diện $S.ABC$ có tam giác $ABC$ vuông tại $B$ và $SA \perp (ABC)$. Chứng minh tứ diện $S.ABC$ có tất cả các mặt là tam giác vuông?

Những câu hỏi liên quan
Cho tứ diện $S.ABC$ có tam giác $ABC$ vuông tại $B$ và $SA$ vuông góc với mặt phẳng $ (ABC)$. Gọi $AH$ là đường cao của tam giác $SBA$. Chứng minh $AH \perp SC.$
SA vuông góc với (ABC)=> SA vuông góc với BC
mà AB vuông góc với BC ( tam giác ABC vuông)
=> BC vg góc với (SAB)=> BC vg góc AH
mà AH vg góc SB
=> AH vg góc (SBC)=> AH vg góc SC
Xem thêm câu trả lời
Cho tứ diện S.ABC có tam giác ABC đều cạnh a , \(SA\perp\left(ABC\right)\) và SA=2a . Gọi \(\left(\alpha\right)\) là mặt phẳng qua B và vuông góc với SC . Tìm thiết diện của tứ diện S.ABC với \(\left(\alpha\right)\) và tính diện tích thiết diện .
Xem chi tiết
Cho hình chóp S.ABC có SA ⊥ (ABC) và AB ⊥ BC. Số các mặt của tứ diện S.ABC là tam giác vuông là:
A. 1
B. 3
C. 4
D. 2
Đáp án C
- Ta có:
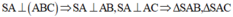 là các tam giác vuông.
là các tam giác vuông.
- Ta có: 
 vuông tại B.
vuông tại B.
- Vậy hình chóp đã cho có cả 4 mặt đều là tam giác vuông.
Đúng 0
Bình luận (0)
Cho tứ diện S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với mặt phẳng đáy. Tính thể tích tứ diện biết đường cao AH của tam giác ABC bằng a và góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) là 60 độ.
Tam giác ABC vuông cân tại A nên \(BC=2AH=2a\)
Từ đó \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}a.2a=a^2\)
Vì \(SA\perp\left(ABC\right);AH\perp BC\) suy ra \(SH\perp BC\)
Do đó : \(\left(\left(SBC\right),\right)\left(ABC\right)=\widehat{SHA}=60^0\)
Suy ra \(SA=AH.\tan60^0=a\sqrt{3}\)
Vậy \(V_{SABC}=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}a\sqrt{3}a^2=\frac{a^3\sqrt{3}}{3}\)
Đúng 0
Bình luận (0)
Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A,
S
A
a
. Gọi
α
là góc giữa hai mặt phẳng
S
B
C
và
A
B
C
bằng A.
3
B.
1
2
C.
2
D. ...
Đọc tiếp
Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A, S A = a . Gọi α là góc giữa hai mặt phẳng S B C và A B C bằng
A. 3
B. 1 2
C. 2
D. 1 3
Đáp án C
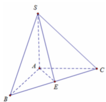
Dựng A E ⊥ B C .
Lại có S A ⊥ A B S A ⊥ A C ⇒ S A ⊥ B C
Do đó B C ⊥ S E A ⇒ S B C ; A B C ⏜ = S E A ⏜
Mặt khác:
A E = B C 2 = a 2 2 ⇒ tan α = t a n S E A ⏜ = S A A E = 2
Đúng 0
Bình luận (0)
Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A, SAa. Gọi
α
là góc giữa hai mặt phẳng (SBC) và (ABC) bằng A.
3
B.
1
2
C.
2
D.
1
3
Đọc tiếp
Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A, SA=a. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC) bằng
A. 3
B. 1 2
C. 2
D. 1 3
Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A, SAa. Gọi
α
là góc giữa hai mặt phẳng (SBC) và (ABC) bằng A.
3
B.
1
2
C.
2
D.
1
3
Đọc tiếp
Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A, SA=a. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC) bằng
A. 3
B. 1 2
C. 2
D. 1 3
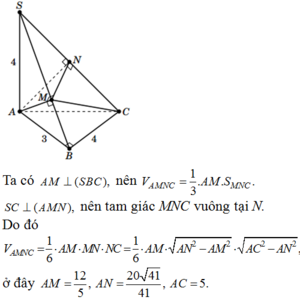
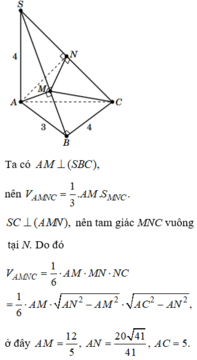
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB 3, BC 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA 4. Gọi AM, AN lần lượt là chiều cao các tam giác SAB và SAC. Thể tích khối tứ diện AMNC là
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3, BC = 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA = 4. Gọi AM, AN lần lượt là chiều cao các tam giác SAB và SAC. Thể tích khối tứ diện AMNC là

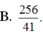
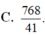
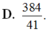
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB 3, BC 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA 4. Gọi AM, AN lần lượt là chiều cao các tam giác SAB và SAC. Thể tích khối tứ diện AMNC là A.
128
41
.
B.
256
41
.
C.
768
41
.
D. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3, BC = 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA = 4. Gọi AM, AN lần lượt là chiều cao các tam giác SAB và SAC. Thể tích khối tứ diện AMNC là
A. 128 41 .
B. 256 41 .
C. 768 41 .
D. 384 41