Đề bài yêu cầu gì?

a) Do ΔABC cân tại A

=> AB = AC; góc ABC=góc ACB

Lại có: góc ABC+ góc ABD = 180^o (kề bù)

góc ACB + góc ACE = 180^o (kề bù)

=> góc ABD = góc ACE

Xét ΔADB và ΔAEC có:

góc BAD = góc CAE (gt)

AB = AC (cmt)

góc ABD = góc ACE (cmt)

=> ΔADB = ΔAEC (g.c.g)

=> BD = CE (2 cạnh tg ứng) đpcm

b) Vì ΔADB = ΔAEC (câu a)

=> góc ADB = góc AEC (2 góc t/ư)

hay góc HDB = góc KEC

Xét ΔBHD vuông tại H và ΔCKE vuông tại E có:

BD = CE (câu a)

góc HDB = góc KEC(cmt)

=> ΔBHD = ΔCKE (ch - gn)

=> BH = CK (2 cạnh tg ứng) (đpcm)

Bài 5:

Tgiac ABC vuông cân tại A => góc CBA = 45 độ

Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB

Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC

=> góc D = 45/2 = 22,5 độ

và góc ACD = 22,5 + 45 = 67,5 độ

Vậy số đo các góc của tgiac ACD là ...

Bài 6: 

Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ

Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ

cmtt với tgiac CBE => góc DEB = 70 độ

=> góc DBE = 180-70-70 = 40 độ

Bài 7: 

Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)

Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C

=> đpcm

Bài 8: mai làm hihi

bài này dễ sao không biết

Bài 8 :
Tự vẽ hình nhé ?
a) Vì ∆ABC cân tại A (GT)
=> ∠ABC = ∠ACB (ĐN)
Mà ∠ABC + ∠DBC = 180^o (2 góc kề bù)
      ∠ACB + ∠ECB = 180^o (2 góc kề bù)
=> ∠DBC = ∠ECB (1)
Xét ∆BCD và ∆CBE có :
BD = CE (GT)
∠DBC = ∠ECB (Theo (1))
BC chung
=> ∆BCD = ∆CBE (c.g.c) (2)
=> ∠BCD = ∠CBE (2 góc tương ứng)
Hay ∠BCI = ∠CBI
Xét ∆IBC có : ∠BCI = ∠CBI (cmt)
=> ∆IBC cân tại I (định lý)
=> IB = IC (ĐN) (3)
Từ (2) => DC = EB (2 cạnh tương ứng)
Mà ID + IC = DC, IE + IB = EB
=> ID = IE
Xét ∆IDE có : ID = IE (cmt)
=> ∆IDE cân tại I (ĐN)
b) Ta có : AB + BD = AD
    Mà AC + CE = AE
          AB = AC (GT)
          BD = CE (GT)
=> AD = AE 
Xét ∆ADE có : AD = AE (cmt)
=> ∆ADE cân tại A (ĐN)
=> ∠ADE = \(\frac{180^o-\widehat{DAE}}{2}\)(4)
Vì ∆ABC cân tại A (GT)
=> ∠ABC = \(\frac{180^o-\widehat{BAC}}{2}\)(5)
Từ (4), (5) => ∠ADE = ∠ABC, mà 2 góc này ở vị trí đồng vị
=> BC // DE (DHNB)
c) Xét ∆ABM và ∆ACM có :
AM chung
AB = AC (GT)
MB = MC (do M là trung điểm của BC)
=> ∆ABM = ∆ACM (c.c.c)
=> ∠AMB = ∠AMC (2 góc tương ứng)
Mà ∠AMB + ∠AMC = 180^o (2 góc kề bù)
=> ∠AMB = ∠AMC = 180^o : 2 = 90^o 
Sau đó chứng minh ∆BIM = ∆CIM theo c.c.c bằng 3 yếu tố MI chung, MB = MC, IB = IC (Theo (3))
Rồi => ∠IMB = ∠IMC (tương ứng)
Mà ∠IMB + ∠IMC = 180^o (kề bù) 
=> ..... (làm như phần trên)
Ta có : ∠AMB + ∠IMB = ∠AMI
Mà ∠AMB = 90^o (cmt)
      ∠IMB = 90^o (cmt)
=> 90^o + 90^o = ∠AMI
=> ∠AMI = 180^o
=> A, M, I thẳng hàng (đpcm)
Vậy .....

cứu mènh:(

Xét ΔBAC và ΔEDC có

CB=CE

\(\widehat{BCA}=\widehat{ECD}\)

CA=CD

Do đó: ΔBAC=ΔEDC

Suy ra: \(\widehat{CDE}=90^0\)

Xét ΔCAB và ΔCDE có 

CA=CD

\(\widehat{ACB}=\widehat{DCE}\)

CB=CE

Do đó: ΔCAB=ΔCDE

Suy ra: \(\widehat{CAB}=\widehat{CDE}\)

hay \(\widehat{CDE}=90^0\)

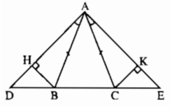
Xét tam giác BHA và ∆CKA có

∠AHB = ∠AKC = 90º

AB = AC ( vì tam giác ABC cân tại A).

∠HAB = ∠KAC ( giả thiết)

Suy ra ΔBHA = ΔCKA (cạnh huyền – góc nhọn), suy ra BH = CK.

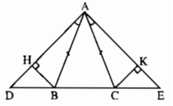
+) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)

Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)

∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)

Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE

+) Xét ΔABD và ΔACE có:

∠DAB = ∠EAC ( giả thiết)

AB = AC (vì tam giác ABC cân tại A)

∠ABD = ∠ACE ( chứng minh trên )

⇒ ΔABD = ΔACE (g.c.g)

⇒ BD = CE ( hai cạnh tương ứng)..

Hình bn tự vẽ nha :))

a) Xét \(\Delta\)ABM và \(\Delta\)ACM, có:   \(\widehat{BAM}=\widehat{CAM};AMchung;\widehat{M=90^o}\) 

=> \(\Delta ABM=\Delta ACM\)(gcg)

=> \(\widehat{ABC}=\widehat{ACB}\)(2g.t.ư); AB=AC ( 2c. t.ư)

b) *Xét \(\Delta\)ABD và \(\Delta\)ACE, có: \(\widehat{ABD}=\widehat{ACE}\)(do  \(\widehat{ABC}=\widehat{ACB}\)); \(AB=AC\)(cmt); \(\widehat{BAD}=\widehat{CAE}\)(gt)

\(\Rightarrow\Delta ABD=\Delta ACE\)(gcg)

* Ta có: \(\widehat{CAD}=\widehat{EAD}-\widehat{CAE};\widehat{BAE}=\widehat{EAD}-\widehat{BAD}\)

Mà \(\widehat{BAD}=\widehat{CAE}\)(gt)    => \(\widehat{CAD}=\widehat{BAE}\)

Xét \(\Delta\)ACD và \(\Delta\)ABE, có: \(\widehat{CAD}=\widehat{BAE}\)(cmt); \(AB=AC\)(cmt); \(\widehat{ACD}=\widehat{ABE}\)

\(\Rightarrow\Delta ACD=\Delta ABE\)(gcg)