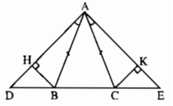
+) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)
Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)
∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)
Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE
+) Xét ΔABD và ΔACE có:
∠DAB = ∠EAC ( giả thiết)
AB = AC (vì tam giác ABC cân tại A)
∠ABD = ∠ACE ( chứng minh trên )
⇒ ΔABD = ΔACE (g.c.g)
⇒ BD = CE ( hai cạnh tương ứng)..









