Xét tam giác BHA và ∆CKA có
∠AHB = ∠AKC = 90º
AB = AC ( vì tam giác ABC cân tại A).
∠HAB = ∠KAC ( giả thiết)
Suy ra ΔBHA = ΔCKA (cạnh huyền – góc nhọn), suy ra BH = CK.
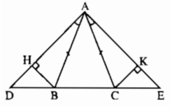
Cho tam giác ABC cân tại A. Trên tia đối BC lấy điểm D, Trên tia đối của tia CB lấy điểm E sao cho ∠BAD = ∠CAE. Kẻ BH vuông góc với AD (H ∈ AD). kẻ CK vuông góc với AE (K ∈ AE). Chứng minh rằng : BD = CE
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho góc BAD= góc CAE. Kẻ BH vuông góc với AD, kẻ CK vuông góc với AE. Chứng minh:
a) BD=CE
b) BH=CK
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia BC lấy điểm E sao cho Goac BAD = Góc CAE. Kẻ BH vuông góc AD ( H thuộc AD). Kẻ CK vuông góc với AE ( K thuộc AE).. CMR
a) BD =CE; b) BH=CK
C
Cho tam giác ABC cân tại A. Trên tia đối BC lấy điểm D, trên tia đối CB lấy điểm E sao cho góc BAD= góc CAE. Kẻ BH vuông góc AD, CK vuông góc AE. Chứng minh:
a/BD=CE
b/ BH=CK
Cho tam giác ABC cân tại A. Trên tia đối BC lấy điểm D, trên tia đối CB lấy điểm E sao cho góc BAD= góc CAE. Kẻ BH vuông góc AD, CK vuông góc AE. Chứng minh:
a/BD=CE
b/ BH=CK
Cho tam giác ABC cân tại A. Trên tia đối của tai BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông với AD, kẻ CK vuông góc với AE. Chứng minh rằng: BH = CK
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD (H∈AD), kẻ CK vuông góc với AE (K∈AE). Chứng minh:
a) BH = CK
b) ∆AHB = ∆AKC
c) BC//HK
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD (H∈AD), kẻ CK vuông góc với AE (K∈AE). Chứng minh:
a) BH = CK
b) ∆AHB = ∆AKC
b) ∆AHB = ∆AKC
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD (H thuộc AD), kẻ CK vuông góc với AE ( K thuộc AE ). Kẻ BM vuông góc với AE (M thuộc AE), kẻ CN vuông góc với AD. Chứng minh rằng:
a) tam giác ADE là tam giác gì?;
b) BH = CK, BM = CN;
c) tam giác AHB = tam giác AKC;
d) BC song song với HK.
