Tìm giá trị x,y thỏa mãn phương trình
a) x2 +y2 = xy
b ) x2 + y2-2(x+2)+5=0
Những câu hỏi liên quan
Cho x; y; z ≠ 0 thỏa mãn x + y + z 0. Tính giá trị biểu thức: A
x
y
x
2
+
y
2
−
z
2
+
y
z
y
2
+...
Đọc tiếp
Cho x; y; z ≠ 0 thỏa mãn x + y + z = 0. Tính giá trị biểu thức: A = x y x 2 + y 2 − z 2 + y z y 2 + z 2 − x 2 + z x z 2 + x 2 − y 2
A. A = 1 2
B. A = - 1 2
C. A = - 3 2
D. A = 3 2
11 tháng 1 2021 lúc 22:48
Cho 2 số thực x ; y thỏa mãn 0 < x ≤ 1 , 0 < y ≤ 1 và x + y = 3xy . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x2 + y2 - 4xy
Cho hai số thực x, y thỏa mãn
x
2
-
y
2
+
1
2
+
4
x
2
y
2
-
x
2
-
y
2
0
. Gọi...
Đọc tiếp
Cho hai số thực x, y thỏa mãn x 2 - y 2 + 1 2 + 4 x 2 y 2 - x 2 - y 2 = 0 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = x 2 + y 2 . Tính M + m
A. M + m = 3
B. M + m = 5
C. M + m = 2
D. M + m = 4
với x,y >0 , thỏa mãn x+4/y ≤ 2 . tìm giá trị lớn nhất của biểu thức P= 2xy/ x2 + y2 + 3xy .
giúp mình với ạ mấy bạn .
Cho hai số x,y \(\ge\)0 thay đổi và thỏa mãn x+y=2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P= x(x3 + x2 + x + 1004y) + y(y3 + y2 + y +1004x) + 1
Cho x; y 0 thỏa mãn log2x + log2y log4( x + y) Tìm x; y để biểu thức P x2 + y2 đạt giá trị nhỏ nhất. A.
x
y
2
3
B.
x
2
3
;
y
2
C. x y 1 D.
y
2
3
;
x
2
2...
Đọc tiếp
Cho x; y > 0 thỏa mãn log2x + log2y = log4( x + y) Tìm x; y để biểu thức P = x2 + y2 đạt giá trị nhỏ nhất.
A. x = y = 2 3
B. x = 2 3 ; y = 2
C. x = y= 1
D. y = 2 3 ; x = 2 2 3
Chọn A.
Theo đầu bài ta có : 2log2xy = log2(x + y) hay x + y = (xy) 2
Đặt u = x + y và v = xy ta có điều kiện u2 - 4v ≥ 0 ; u > 0; v > 0.
Mà u = v2 nên v4 - 4v ≥ 0 suy ra 
Ta có P = v4 - 2v = g(v) với 
Đạo hàm g’(v) = 4v3-2 > 0 với mọi 
nên 
khi 
Đúng 0
Bình luận (0)
Cho x; y 0 thỏa mãn log 2x+ log2ylog4(x+y) Tìm x; y để biểu thức P x2+y2 đạt giá trị nhỏ nhất. A.
x
y
2
3
B.
x
2
3
;
y
2
C. xy1 D.
y
2
3
;
x
2
2
3
Đọc tiếp
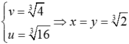
Cho x; y> 0 thỏa mãn log 2x+ log2y=log4(x+y) Tìm x; y để biểu thức P= x2+y2 đạt giá trị nhỏ nhất.
A. x = y = 2 3
B. x = 2 3 ; y = 2
C. x=y=1
D. y = 2 3 ; x = 2 2 3
Theo đầu bài ta có: log 2x+ log2y=log4(x+y) hay 2 log 2(xy) =log2(x+y)
Suy ra x+y=(xy) 2
Đặt u= x+ y; v= xy ta có điều kiện u2-4v≥0; u>0; v>0 .
Mà 
Ta có
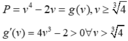
nên minP=
2
4
3
khi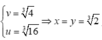 
Chọn A.
Đúng 0
Bình luận (0)
Cho số phức
z
x
+
y
i
(
x
,
y
∈
R
)
thỏa mãn
z
-
2
+
i
z
+
2
+
5
i
và biểu thức
H
x...
Đọc tiếp
Cho số phức z = x + y i ( x , y ∈ R ) thỏa mãn z - 2 + i = z + 2 + 5 i và biểu thức H = x 2 + y 2 - 3 y + 1 x 2 + y 2 + 2 x - 2 y + 2 x 2 + y 2 - 2 x - 4 y + 5 đạt giá trị nhỏ nhất. Giá trị của 2x + y bằng
A. -6
B. - 6 + 5
C. - 3 - 5
D. - 6 - 5
Biết x2+4y2+9z2=3 Tìm GTLN của S=2x+4y+6x
Cho x;y ∈ 𝑅 thỏa mãn x2+y2 -xy=4 . Tìm giá trị lớn nhất và nhỏ nhất của C= x2+y2
a) Áp dụng bất đẳng thức Cosi ta có :
\(x^2+1\geq 2x\\ 4y^2+1\geq 4y\\ 9z^2+1\geq 6z\)
Suy ra \(S\leq 6\)
Dấu = xảy ra khi \(x=1;y=\frac{1}{2}; z=\frac{1}{3}\)
Đúng 0
Bình luận (0)