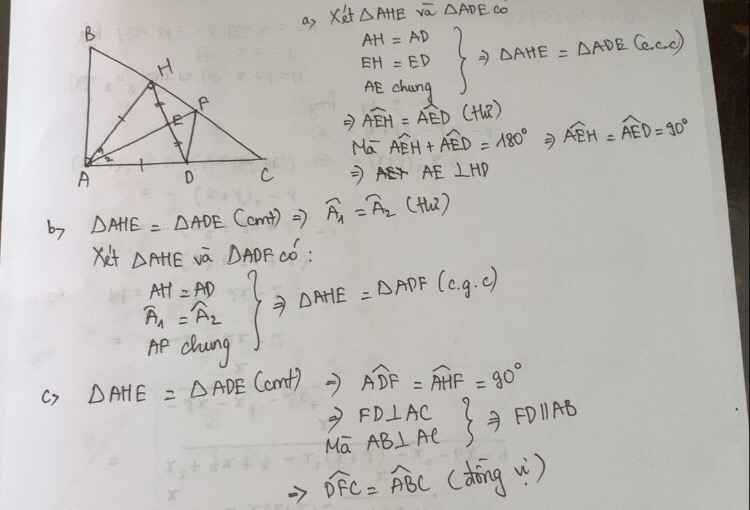cho tam giac ABC vuông tại A lấy D sao cho AD=AH gọi E là trung điểm của HD .tia AE cắt BC tại F a) chứng minh tam giác AHE = tam giác ADE , cm AE VUÔNG hd b)cm tam giác AHF = tam giác ADE

Những câu hỏi liên quan
cho tam giác abc vuông tại A (AB<AC) ke Ah vuông với bc tại h trê cạnh ac lấy điểm d sao cho ad=ah gọi e là trung điểm của hd tia ae cắt bc tai f cm a) tam giác ahe= tam giác ade và ae vuông tại hd b) tam giác ahf = tam giác adf c) góc dfc= góc abc
cho tam giác abc vuông tại A (AB<AC) ke Ah vuông với bc tại h trê cạnh ac lấy điểm d sao cho ad=ah gọi e là trung điểm của hd tia ae cắt bc tai f cm a) tam giác ahe= tam giác ade và ae vuông tại hd b) tam giác ahf = tam giác adf c) góc dfc= góc abc
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Trên cạnh AC lấy D sao cho AD = AH. Gọi E là trung điểm của HD. Tia AE cắt BC tại F. Chứng minh rằng:
𝑎)∆𝐴𝐻𝐸 = ∆𝐴𝐷𝐸; 𝐴𝐸 𝑣𝑢ô𝑛𝑔 𝑔ó𝑐 𝑣ớ𝑖 𝐻𝐷.
b) ∆𝐴𝐻𝐹 = ∆𝐴𝐷𝐹
𝑐)𝐷𝐹𝐶 ̂ = 𝐴𝐵𝐶 ̂
(có vẽ hình)
a: Xét ΔAHE và ΔADE có
AH=AD
HE=DE
AE chung
Do đó: ΔAHE=ΔADE
Đúng 0
Bình luận (0)
Cho tam giac ABC vuông tại A, co B= 60°. Vẽ AH vuông góc BC tại H.
a, Tính HAB
b, Trên cạnh AC lấy D sao cho AD= AH. Gọi I là trung điểm cua cạnh HD. CM: tam giac AHI = ADI
c, Tia AI cắt cạnh HC tại K. CM: tam giác AHK = ADK, AB son song KD
d, Trên tia đối của tia HA lấy E sao cho HE =HA. CM: H là trung điểm BK và 3 điểm D,K,E thẳng hàng
a, TG HAB có :
BAH + BHA + B = 180
=> BAH + 90 + 60 = 180
=> HAB = 30
Đúng 0
Bình luận (0)
b,chứng minh tam giác AHI và tam giác ADI bằng nhau đúng ko
Xét TG AIH và TG AID có :
AH = AD (gt)
AI cạnh chung
HI = ID (gt)
=> TG AIH = TG AID (c-c-c)
Đúng 0
Bình luận (0)
A)tính thành hai Trung đ
Xét các vế AB và CT
B)tính các tia đối...??
C...??? Tương tự
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, có góc B = 60 độ. Vẽ AH vuông góc với BC tại H. Trên AC lấy điểm D sao cho AD = AH. Gọi I là trung điểm của HD. Tia AI cắt HC tại K. Trên tia đối của HA lấy E sao cho HE = HA. Chứng minh H là trung điểm của BK
Vẽ nháp bằng tay, hình không đẹp cho lắm :v Bài viết có hơi lỗi.
Bài toán phụ : Chứng minh tam giác vuông có 1 góc 60 độ thì cạnh góc vuông nhỏ hơn sẽ bằng 1 nửa cạnh huyền.
Tam giác MNP vuông tại M có góc N là 60 độ.
Trên tia đối tia MN lấy điểm Q sao cho MQ=MN
Tam giác NPQ có PM vừa là trung tuyến vừa là đường cao nên cân tại P, mà lại có 1 góc 60 độ nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều), từ đó suy ra NQ = NP, mà NQ= 2MN nên MN = \(\frac{1}{2}\)NP, bài toán được chứng minh.
Tương tự với bài toán của chúng ta :
\(\Delta ABC\)vuông tại Acó \(\widehat{B}=60^o\) \(\Rightarrow AB=\frac{1}{2}BC\)
\(\Delta ABH\)vuông tại H có \(\widehat{B}=60^o\) \(\Rightarrow HB=\frac{1}{2}AB\)
\(\Rightarrow HB=\frac{1}{4}BC\)
Trước hết \(\Delta ABH\) vuông tại H có \(\widehat{B}=60^o\)
nên \(\widehat{HAB}=90^o-60^o=30^o\)Mà \(\widehat{DAH}+\widehat{HAB}=\widehat{BAC}=90^o\)
\(\Rightarrow\widehat{DAH}=60^o\)
\(\Delta DAH\)cân tại A ( AD = AH ), có góc DAH là 60o nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều )
Như vậy AI là đường cao đồng thời cũng là phân giác góc DAH
\(\Rightarrow\widehat{IAH}=\frac{1}{2}\widehat{DAH}=\frac{60^o}{2}=30^o\)
\(\Rightarrow\widehat{KAB}=\widehat{IAH}+\widehat{HAB}=30^o+30^o=60^o\)
\(\Delta KAB\)có \(\widehat{KAB}=\widehat{KBA}=60^o\) nên là tam giác đều
\(\Rightarrow KB=AB\)
Mà \(HB=\frac{1}{2}AB\Rightarrow HB=\frac{1}{2}KB\), hay H là trung điểm của KB.
Vậy ....
Đúng 0
Bình luận (0)
bạn ấy làm đúng rồi, nhưng có vẻ bạn ấy làm cách áy là hơi dài nhỉ ?
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A. Trên tia đối AB lấy điểm E sao cho AC = AE. Trên tia đối AC lấy điểm D sao cho AD =AB. Kẻ AH vuông BC tại H, tia HA cắt DE tại F. Cm F là trung điểm DE.
Cho tam giác ABC vuông tại A, đường cao AH, biết AB=15cm, AC=20cm. a) Tính BC, AH. b) Trên đoạn HC lấy D sao cho HD=HB. Tính tanADH và chứng minh: HD.HC=HA^2. c) Trên tia AH lấy E sao cho H là trung điểm của AE. Đường thẳng ED cắt AC tại F. Gọi O là trung điểm của CD. Chứng minh: HF vuông FO d) Đoạn HF cắt AD tại S. Tia CS cắt AH tại K và cắt AB tại M.CM: AB/AM + AD/AS= AE.AK
Cho tam giác ABC vuông tại A, có góc B = 60 độ. Vẽ AH vuông góc với BC tại H. Trên AC lấy điểm D sao cho AD = AH. Gọi I là trung điểm của HD. Tia AI cắt HC tại K. Trên tia đối của HA lấy E sao cho HE = HA. Chứng minh H là trung điểm của BK
cho tam giác ABC đường cao AH
a trên cạnh ac lấy d sao cho ad =ah từ d kẻ đường thẳng vuông góc với ac cắt bc tại e . Gọi i là giao đỉ của AE và HD . chứng minh tam giác ahe = tam giác ade và ih =id
lấy f là giao điểm của ahvaf de ,k là trung điểm của cf . chứng minh tam giác efc cân và i e k thẳng hàng
a: Xét ΔAHE vuông tại H và ΔADE vuông tại D có
AE chung
AH=AD
=>ΔAHE=ΔADE
=>HE=DE và góc EAH=góc DAE
=>AE là phân giác của góc DAH
AH=AD
EH=ED
=>AE là trung trực của HD
=>I là trung điểm của HD
=>IH=ID
b: Xét ΔEHF vuông tại H và ΔEDC vuông tại D có
EH=ED
góc HEF=góc DEC
=>ΔEHF=ΔEDC
=>EF=EC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Gọi H là trung điểm BC. Từ H kẻ HD vuông góc AB tại D và HE vuông góc với AC tại E. a/ Chứng minh: tam giac HDB = tam giacHEC b/ Chứng minh : AD=AE. c/ Qua A kẻ đường thẳng xy song song BC, tia HD cắt xy tại M, tia HE cắt xy tại N. Chứng minh tam giác HMN là tam giác cân?
giup tui voii tks nhieuu
a: Xét ΔHDB vuông tại D và ΔHEC vuông tại E có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHDB=ΔHEC
b: Ta có: ΔHDB=ΔHEC
nên BD=EC
Ta có: AD+DB=AB
AE+EC=AC
mà BD=CE
và AB=AC
nên AD=AE
Đúng 1
Bình luận (0)