Xét tam giác đều ABC có

G là trọng tâm của tam giác(gt)

=> 3 đường trung tuyến bằng nhau

=> \(GB=GC=AG=\dfrac{2}{3}AM=\dfrac{2}{3}.3=2\left(cm\right)\)

Vì ΔBAC đều nên \(GB=GC=\dfrac{2}{3}AM\)

hay GB=GC=2cm

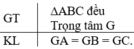
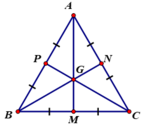
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.

Khi đó AM, BN, CP đồng quy tại trọng tâm G.

Ta có: ∆ABC đều suy ra:

+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).

+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).

⇒ AM = BN = CP (1)

Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:

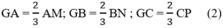
Từ (1) , (2) ⇒ GA = GB = GC.

GA=GB=GC, G là trọng tâm tam giác kkhi và chỉ khi đso là tam giác đều. 

Đề sai

\(\overrightarrow{GA}+\overrightarrow{GB}-\overrightarrow{GC}\)

\(=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{CG}\)

\(=\overrightarrow{GA}+\overrightarrow{CB}\)

Qua C, lấy K sao cho \(\overrightarrow{CK}=\overrightarrow{GA}\)

=>CK//GA và CK=GA

Xét ΔABC đều có G là trọng tâm

nên AG⊥BC

=>CK⊥CB

Xét ΔABC đều có G là trọng tâm

nên G là tâm đường tròn ngoại tiếp ΔABC

=>GA=GB=GC

Xét (G) có \(\hat{BAC}\) là góc nội tiếp chắn cung BC

nên \(\hat{BGC}=2\cdot\hat{BAC}=120^0\)

Xét tứ giác AGCK có

AG//CK

AG=CK

Do đó: AGCK là hình bình hành

Hình bình hành AGCK có AG=GC

nên AGCK là hình thoi

=>CA là phân giác của góc GCK

=>\(\hat{GCK}=2\cdot\hat{GCA}=60^0\)

Xét ΔGCK có GC=KC và \(\hat{GCK}=60^0\)

nên ΔGCK đều

=>\(\hat{KGC}=60^0\)

\(\hat{BGC}+\hat{KGC}=120^0+60^0=180^0\)

=>B,G,K thẳng hàng

Trên tia đối của tia GC, lấy E sao cho GC=GE

=>G là trung điểm của EC

Ta có: EC=2GC

BK=2GB

mà GC=GB

nên EC=BK

Xét tứ giác BCKE có

G là trung điểm chung của BK và CE

=>BCKE là hình bình hành

Hình bình hành BCKE có \(\hat{BCK}=90^0\)

nên BCKE là hình chữ nhật

=>\(\overrightarrow{CB}+\overrightarrow{CK}=\overrightarrow{CE}=2\cdot\overrightarrow{CG}\)

\(\overrightarrow{GA}+\overrightarrow{CB}=\overrightarrow{CK}+\overrightarrow{CB}=2\cdot\overrightarrow{CG}\)

=>\(\overrightarrow{GA}+\overrightarrow{GB}-\overrightarrow{GC}=2\cdot\overrightarrow{CG}\)