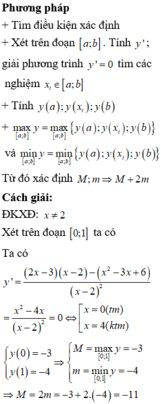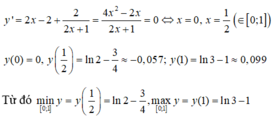Tìm giá trị nhỏ nhất của hàm số y= x2(1-6x)

Những câu hỏi liên quan
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bạc hai y = -2x2 + 4x + 3
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = -3x2 + 2x + 1 trên (1;3)
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = x2 - 4x - 5 trên (-1;4)
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Đúng 0
Bình luận (0)
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
Đúng 0
Bình luận (0)
Câu 3:
$y=x^2-4x-5$ có $a=1>0, b=-4; c=-5$ có trục đối xứng $x=\frac{-b}{2a}=2$
Do $a>0$ nên hàm nghịch biến trên $(-\infty;2)$ và đồng biến trên $(2;+\infty)$
Với $x\in (-1;4)$ vẽ BTT ta thu được $y_{\min}=f(2)=-9$
Đúng 0
Bình luận (0)
Giá trị nhỏ nhất của hàm số y
-
x
2
+
x
-
6
x
+
1
trên đoạn [0;3] bằng: A. -6 B. -3 C. 3 -
4
2
D. 3 +
4
2
Đọc tiếp
Giá trị nhỏ nhất của hàm số y = - x 2 + x - 6 x + 1 trên đoạn [0;3] bằng:
A. -6
B. -3
C. 3 - 4 2
D. 3 + 4 2
Chọn C
Lưu ý: Hàm số liên trục trên một Đoạn thì luôn có GTLN và GTNN trên đoạn đó Nên áp dụng bài toán tìm GTLN, GTNN của hàm số trên một đoạn, không lập BBT của hàm sô.
Hàm số y = - x 2 + x - 6 x + 1 liên tục trên đoạn [0;3]
![]()
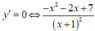

![]()
![]()
![]()
Đúng 0
Bình luận (0)
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
-
x
2
+
6
x
-
5
trên đoạn [1;5] lần lượt là A. 2 và 0 B. 4 và 0 C. 3 và 0 D. 0 và -2
Đọc tiếp
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - x 2 + 6 x - 5 trên đoạn [1;5] lần lượt là
A. 2 và 0
B. 4 và 0
C. 3 và 0
D. 0 và -2
Đáp án A.
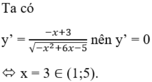
Vì y(1) = y(5) = 0 và y(3) = 2 nên giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [1;5] lần lượt là 2 và 0
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của hàm số y= x2-6x
y = x^2 -6x
Do y là số chưa biết mà muốn chuyển thì kết quả là: \(\infty\)
Đúng 4
Bình luận (0)
gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y=2\(\sqrt{7+6x-(x)^{2}}\)+x2 -6x +2014.Tính tổng các giá trị nguyên của a thuộc đoạn [m,M]
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
2
-
3
x
+
6
x
-
2
trên đoạn [ 0;1]. Giá trị của M +2m bằng A.
-
11
B.
-
10
C. 11 D. 10
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 - 3 x + 6 x - 2 trên đoạn [ 0;1]. Giá trị của M +2m bằng
A. - 11
B. - 10
C. 11
D. 10
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
2
-
3
x
+
6
x
-
2
trên đoạn [0;1]. Giá trị của M+2m bằng A. -11 B. -10 C. 11 D. 10
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 - 3 x + 6 x - 2 trên đoạn [0;1]. Giá trị của M+2m bằng
A. -11
B. -10
C. 11
D. 10
ĐKXĐ: x#2
Xét trên đoạn [0;1]
Ta có
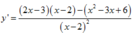
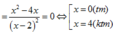
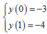
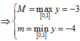
![]()
Chọn đáp án A.
Đúng 0
Bình luận (0)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
2
-
3
x
+
6
x
-
2
trên đoạn [0;1]. Giá trị của M + 2m bằng A. -11 B. -10 C. 11 D. 10
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 2 - 3 x + 6 x - 2 trên đoạn [0;1]. Giá trị của M + 2m bằng
A. -11
B. -10
C. 11
D. 10
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
x
2
-
2
x
+
l
n
(
2
x
+
1
)
trên [0; 1] A.
m
a
x
0
;
1
y
ln
3
+
1
;
m...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 2 - 2 x + l n ( 2 x + 1 ) trên [0; 1]
A. m a x 0 ; 1 y = ln 3 + 1 ; m i n 0 ; 1 y = ln 2
B. m a x 0 ; 1 y = ln 3 - 1 ; m i n 0 ; 1 y = 0
C. m a x 0 ; 1 y = ln 3 - 1 ; m i n 0 ; 1 y = ln 2 - 3 4
D. m a x 0 ; 1 y = ln 2 + 3 4 ; m i n 0 ; 1 y = ln 3 - 1