Đáp án A.
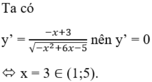
Vì y(1) = y(5) = 0 và y(3) = 2 nên giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [1;5] lần lượt là 2 và 0
Đáp án A.
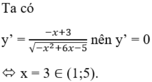
Vì y(1) = y(5) = 0 và y(3) = 2 nên giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [1;5] lần lượt là 2 và 0
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 4 - 2 x 3 + 3 trên đoạn [0; 2]. Tính giá trị của biểu thức M + 2m.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) liên tục trên (0;+ ∞ ) thỏa mãn 3x.f(x) - x 2 f ' ( x ) = 2 f 2 ( x ) , với f(x) ≠ 0, ∀ x ∈ (0;+ ∞ ) và f(1) = 1 3 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Tính M + m.
A. 9 10
B. 21 10
C. 7 3
D. 5 3
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) cho như hình vẽ.
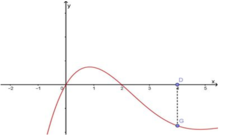
Biết rằng f(2) + f(4) = f(3) + f(0). Giá trị nhỏ nhất và lớn nhất của f(x) trên đoạn [0;4] lần lượt là
A. f(2), f(0)
B. f(4), f(2)
C. f(0), f(2)
D. f(2), f(4)
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
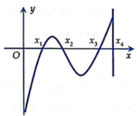
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 + 3 x 2 - 9 x + 1 trên đoạn [0; 3] lần lượt bằng
A. 25 và 0
B. 36 và -5
C. -28 và -4
D. 54 và 1
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
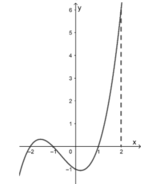
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
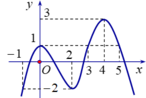
Cho hàm số f(x) liên tục trên đoạn [-1;5] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên [-1;5]. Giá trị của M-m bằng ?
A. 4
B. 1
C. 6
D. 5
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = e x 2 - 2 x + 3 trên đoạn [0 ; 2] là:
A . e 3 -e
B. e 3 + e 2
C . e 3
D. e 3 +e
Tính giá trị lớn nhất và nhỏ nhất của hàm số:
y = x 4 - 3 x 2 + 2 trên các đoạn [0; 3] và [2; 5]