cho tam giác ABC , M là trung điểm của BC , biết AM=BC. chứng minh tam giác ABC vuông tại A

Những câu hỏi liên quan
Cho tam giác ABC ,M là trung điểm của BC , biết AM = 1/2 BC . Chứng minh tam giác ABC vuông tại A
cho tam giác ABC lấy M là trung điểm của cạnh BC
biết AM=1/2 BC chứng minh tam giác ABC vuông tại A
\(AM=\frac{BC}{2}\Rightarrow AM=BM=CM\)
=> tg ABM cân tại M \(\Rightarrow\widehat{ABC}=\widehat{BAM}\)
Và tg ACM cân tại M \(\Rightarrow\widehat{ACB}=\widehat{CAM}\)
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=\widehat{BAM}+\widehat{CAM}=\widehat{BAC}\)
Mà \(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{BAC}=\widehat{BAC}\Rightarrow\widehat{BAC}=90^o\)
=> tg ABC vuông tại A
Cho tam giác abc cân tại a . M là trung điểm của bc . Mi vuông góc vs ab . Mk vuông góc vs ac. - chứng minh tam giác BIM = tam giác BKM - chứng minh AM là đường trung trực của BC - Tính BC biết Ab = 10 cm , AM =8cm
a)
Sửa đề: ΔBIM=ΔCKM
Xét ΔBIM vuông tại I và ΔCKM vuông tại K có
BM=CM(M là trung điểm của BC)
\(\widehat{IBM}=\widehat{KCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBIM=ΔCKM(cạnh huyền-góc nhọn)
Đúng 1
Bình luận (1)
cho tam giác ABC , M là trung điểm của BC Chứng minh nếu 2.AM =BC thì tam giác ABC vuông tại A
Ai giúp mình với !!!
a) Cho tam giác ABC, kẻ AH vuông góc với BC, nối A với trung điểm M của BC. Biết góc BAH = góc HAM = góc MAC và AB<AC. Tính số đo các góc của tam giác ABC.
b) Chứng minh rằng tam giác ABC vuông tại A. M là trung điểm của BC. Chứng minh AM = MB = MC.
Cho tam giác ABC có AB = AC , M là trung điểm của BC.
a ) Chứng minh : Tam giác ABM bằng tam giác ACM .
b) Chứng minh : AM là tia phân giác của góc BAC.
c ) Chứng minh : AM vuông góc với BC tại M. giúp mik vs
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Đúng 0
Bình luận (0)
\(a,\) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (giả thiết)
\(AM\) là cạnh chung
\(BM=CM\) (giả thiết)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
\(b,\) Vì \(\Delta ABM=\Delta ACM\) (chứng minh câu \(a\))
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) (\(2\) góc tương ứng)
\(\Rightarrow AM\) là tia phân giác \(\widehat{BAC}\)
\(c,\) Vì \(\Delta ABC\) cân tại \(A\) (giả thiết)
Mà \(AM\) là tia phân giác \(\widehat{BAC}\) (chứng minh câu \(b\))
\(\Rightarrow AM\) là đường trung trực \(\Delta ABC\)
\(\Rightarrow AM\perp BC\) tại \(M\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, M trung điểm BC N đối xứng với M qua AB. a)Chứng minh AMBN là hình thoi
b) Chứng minh ACMN là hình bình hành. I trung điểm AM. Chứng minh 3 điểm, N,I,C thẳng hàng.
c)Biết AC=6cm,AM=5cm. tính BC,AB và diện tích tam giác ABC
giải chi tiết mn ạ
a: M đối xứng N qua AB
nên AM=AN; BM=BN
mà MA=MB
nên MA=MB=AN=BN
=>AMBN là hình thoi
b: Xét tứ giác ACMN có
AN//CM
AN=CM
Do đó: ACMN là hình bình hành
=>AM cắt CN tại trung điểm của mỗi dường
=>N,I,C thẳng hàng
c: BC=2*AM=10cm
=>AB=8cm
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Lấy M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh rằng a) tam giác ABC= tam giác CDA b) AM=½BC
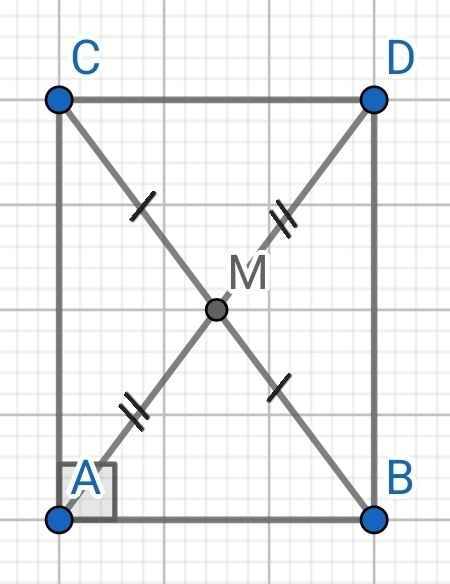
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆AMB và ∆DMC có:
AM = DM (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆AMB = ∆DMC (c-g-c)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
Lại có:
∠MAC + ∠MAB = 90⁰ (∆ABC vuông tại A)
⇒ ∠MAC + ∠MDC = 90⁰
⇒ ∠DAC + ∠ADC = 90⁰
∆CDA có:
∠DAC + ∠CDA + ∠ACD = 180⁰ (tổng ba góc trong ∆ACD)
⇒ ∠ACD = 180⁰ - (∠DAC + ∠CDA)
= 180⁰ - 90⁰
= 90⁰
⇒ ∆ACD vuông tại C
Do ∆AMB = ∆DMC (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABC và ∆CDA có:
AC là cạnh chung
AB = CD (cmt)
⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)
b) Do ∆ABC = ∆CDA (cmt)
⇒ BC = AD (hai cạnh tương ứng)
Do AM = DM (gt)
⇒ AM = DM = ½AD
Mà AD = BC (cmt)
⇒ AM = ½BC
Đúng 1
Bình luận (0)
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
DO đó: ABDC là hình bình hành
Suy ra: AB=DC; AC=BD
Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=1/2BC
Đúng 2
Bình luận (0)
Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
a)

Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=>\(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông)
=> AC=AB (2 cạnh tương ứng)
=> Tam giác ABC cân tại A
b)

Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGM có:
AM chung
\(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC)
=>\(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM (giả thiết)
MH=MG(chứng minh trên)
=>\(\Delta BHM = \Delta CGM\)(cạnh huyền – cạnh góc vuông)
=>\(\widehat {HBM} = \widehat {GCM}\)(2 góc tương ứng)
=>Tam giác ABC cân tại A.
Đúng 0
Bình luận (2)


















