1. Cho tam giác ABC cân tại A ; A( 3,2) ; B( 4 ; -1 ) ; gọi H là trung điểm BC . Tìm tọa độ điểm C
2. Cho tam giác ABC có A ( 3 ; 2) ; B(4;-1) ; C(5,7) . Tìm tọa độ trực tâm H
Mọi người ơi ! giải giúp em với ạ ! mai kt rồi
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh rằng :HB=HC
b) Chứng minh rằng: AH là tia phân giác của góc A
Bài 2: Cho tam giác ABC cân tại A có góc A < 90 độ. Vẽ BM vuông góc với AC tại M, CN vuông góc với AB tại N
a) Chứng minh AM= AN
b) Gọi I là giao điểm của BM và CN. Chứng minh rằng AI là tia phân giác của góc A.
Cho tam giác ABC cân tại A. Tia phân giác góc A cẳ BC tại D
a) Chứng minh rắng: Tam giác ADB = tam giác ADC
a: Xét ΔADB và ΔADC có
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
AB=AC
Do đó: ΔADB=ΔADC
Xét `2 Delta ADB, ADC`:
`AD` chung
`AB = AC`.
`hat(DAB) = hat(DAC)`
`=> Delta ADB = Delta ADC`.
Xét △ADB và △ADC có:
AD: chung
∠BAD = ∠CAD(AD là tai phân giác)
AB=AC( vì △ABC cân tại A)
⇒ △ADB = △ADC(c.g.c)
Cho tam giác ABC về phía ngoài của tam giác vẽ tam giác BAD vuông cân tại A và tam giác CAE vuông cân tại A.
a) CMR: Đường trung tuyến AM của tam giác ABC vuông góc với DE tại K
b) CMR: Đường cao AH của tam giác ABC đi qua tđ N của DE
Tớ sẽ cho 4 tick, tớ hứa
Cho tam giác ABC ( góc A < 90 độ) . Vẽ ra phía ngoài tam giác ABC các tam giác vuông cân (cân tại A) Và AEC (cân tại A)
a, CMR : BE=CD
b, Cmr : BE vuông góc với CD
Câu 1 cho tam giác ABC cân tại A có \(\widehat{A}̣\)=20 độ ,vẽ tam giác đều DBC(D nằm trong tam giác ABC). Tia phân giác của góc ABD cắt AC tại M.Chứng minh AM=BC
mk gặp dạng bài này rồi!
bài này bạn phải vẽ chuẩn nha ko là sai đấy
cho tam giác abc cân tại a tia phân giác góc a cắt bc tại i
a)chứng minh rằng tam giác abi bằng tam giác aci
b) tính góc bia
a) Xét \(\Delta ABI\) và\(\Delta ACI\) có
góc B= góc C(gt)
AB=AC(gt)
góc BAI =góc CAI(AI là p/g góc A)
Vậy \(\Delta ABI\) =\(\Delta ACI\) (g.c.g)
a) Xét ΔABI và ΔACI có
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
AB=AC(ΔABC cân tại A)
\(\widehat{BAI}=\widehat{CAI}\)(AI là tia phân giác của \(\widehat{BAC}\)
Do đó: ΔABI=ΔACI(g-c-g)
b) Ta có: ΔABI=ΔACI(cmt)
nên \(\widehat{AIB}=\widehat{AIC}\)(hai góc tương ứng)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
Vậy: \(\widehat{BIA}=90^0\)
Các cậu giúp tớ bài này với ạ
Cho tam giác ABC về phía ngoài của tam giác vẽ tam giác BAD vuông cân tại A và tam giác CAE vuông cân tại A.
a) CMR: Đường trung tuyến AM của tam giác ABC vuông góc với DE tại K
b) CMR: Đường cao AH của tam giác ABC đi qua tđ N của DE
Tớ sẽ cho 4 tick, tớ hứa
bạn lên học 24 đi nhiều người giỏi lắm . t hen
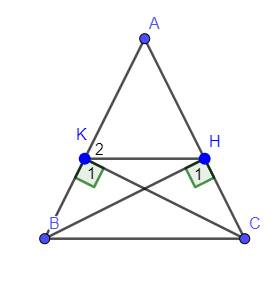
cho tam giác ABC cân tại A ( A < 90˚ ) kẻ BC vuông góc với AC tại H , CK vuông góc với AB tại K
a) chứng minh hai tam giác BHC = CKB từ đó tam giác AHK cân
b) chứng minh BC // HK
`a)`
+, Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=hat(ACB)`
hay `hat(KBC)=hat(HCB)`
Xét `Delta BHC` và `Delta CKB` có :
`{:(hat(H_1)=hat(K_1)(=90^0)),(BC-chung),(hat(HCB)=hat(KBC)(cmt)):}}`
`=>Delta BHC=Delta CKB(c.h-g.n)(đpcm)`
+, Có `Delta BHC=Delta CKB(cmt)`
`=>HC=BK` ( 2 cạnh t/ứng )
mà `AB=AC(Delta ABC` cân tại `A)`
nên `AB-BK=AC-CH`
hay `AK=AH`
`=>Delta AHK` cân tại `A(đpcm)`
`b)`
Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2` (1)
`Delta AHK ` cân tại `A(cmt)=>hat(K_2)=(180^0-hat(A))/2` (2)
Từ (1) và (2) suy ra :
`hat(ABC)=hat(K_2)`
mà `2` góc này ở vị trí Đồng vị
nên `KH////BC(đpcm)`
Cho tam giác ABC cân tại A .Vẽ phân giác trong của góc B, và phân giác ngoài của góc A, chúng cắt nhau tại I .Chứng minh rằng AI// BC và tam giác ABI cân
Bài 1: Cho tam giác ABC cân tại A,vẽ AH vuông góc với BC tại H. Biết AB=10cm, BH=6cm
a)Tính AH
b)CM: Tam giác ABH=tam giác ACH
c)Trên BA lấy D, CA lấy E sao cho BD=CE.CM tam giác HDE cân
d)CM:AH là trung trực của DE
Bài 2: Cho tam giác ABC cân tại A.Kẻ BD vuông góc với AC,CE vuông góc với AB. BD cắt CE cắt nhau tại H
a)Tam giác ADB=tam giác ACE
b)Tam giác AHC cân
c)ED song song BC
d)AH cắt BC tại K, trên HK lất M sao cho K là trung điểm của HM.CM tam giác ACM vuông
Bài 3:Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ DE vuông góc với BC(E thuộc BC.Gọi F là giao điểm của BA và ED.CMR:
a)tam giác ABD=tam giác EBD
b)Tam giác ABE là tam giác cân
c)DF=DC
Bài 4: Cho tam giác ABC có góc A=90 độ,AB=8cm,AC=6cm
a) Tính BC
b)Trên cạnh AC lấy điểm E sao cho AE=2cm,trên tia đối của tia AB lấy D sao cho AD=AB.CM: tam giác BEC=tam giác DEC
c)CM: DE đi qua trung điểm cạnh BC