\(\text{#3107}\)

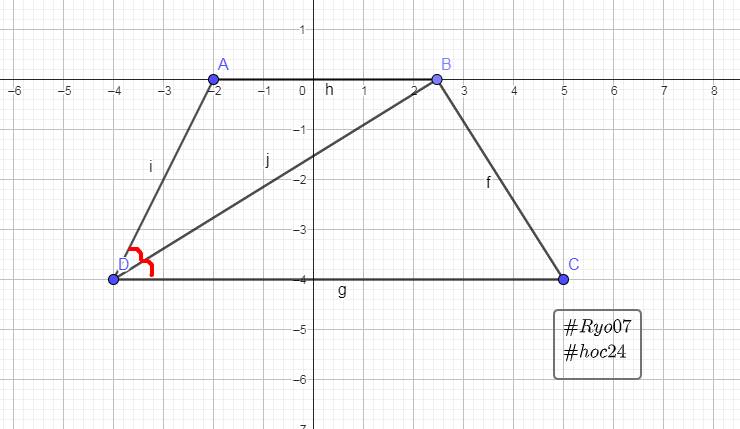
a)

Vì BD là tia phân giác của \(\widehat{\text{ADC}}\)

\(\Rightarrow\widehat{\text{ADB}}=\widehat{\text{CDB}}=\dfrac{1}{2}\widehat{\text{ADC}}\)

Mà ABCD là hình thang cân

\(\Rightarrow\widehat{\text{C}}=\widehat{\text{D}}\)

\(\Rightarrow\widehat{\text{C}}=2\widehat{\text{BDC}}\)

Xét `\Delta BDC:`

\(\widehat{\text{BDC}}+\widehat{\text{CBD}}+\widehat{\text{C}}=180^0\\ \Rightarrow\widehat{\text{BDC}}+90^0+2\widehat{\text{BDC}}=180^0\\ \Rightarrow3\widehat{\text{BDC}}=90^0\\ \Rightarrow\widehat{\text{BDC}}=30^0\)

Vì \(\widehat{\text{C}}=2\widehat{\text{BDC}}\)

\(\Rightarrow\widehat{\text{C}}=2\cdot30^0\\ \Rightarrow\widehat{\text{C}}=60^0\)

Vì $\widehat{C} = \widehat{D}$

\(\Rightarrow\widehat{\text{C}}=\widehat{\text{D}}=60^0\)

Vì ABCD là hình thang cân

\(\Rightarrow\widehat{\text{A}}+\widehat{\text{D}}=180^0\left(\text{2 góc trong cùng phía bù nhau}\right)\\ \Rightarrow\widehat{\text{A}}+60^0=180^0\\ \Rightarrow\widehat{\text{A}}=120^0\)

Vì \(\widehat{\text{A}}=\widehat{\text{B}}\left(\text{ABCD là hình thang cân}\right)\)

\(\Rightarrow\widehat{\text{A}}=\widehat{\text{B}}=120^0\)

Vậy, số đo các góc trong hình thang cân ABCD là: \(\widehat{\text{A}}=\widehat{\text{B}}=120^0;\widehat{\text{C}}=\widehat{\text{D}}=60^0.\)

 Xét dãy số \(u_n=S_{A_nB_nC_nD_n}\). Ta có \(u_1=a^2\)

 Ta xét hình vuông có cạnh \(x\) (diện tích là \(x^2\)). Khi đó nửa độ dài đường chéo của hình vuông này sẽ là \(\dfrac{x}{\sqrt{2}}\). Khi đó diện tích của hình vuông mới là \(\left(\dfrac{x}{\sqrt{2}}\right)^2=\dfrac{x^2}{2}\) bằng 1 nửa diện tích hình vuông ban đầu. Như vậy, ta có mối quan hệ truy hồi: \(u_{n+1}=2u_n\). Dễ thấy đây là một cấp số nhân.

 Ta có \(\left(u_n\right):\left\{{}\begin{matrix}u_1=a^2\\u_{n+1}=2u_n\end{matrix}\right.\) 

\(\Rightarrow S_n=\sum\limits^{\infty}_{i=1}u_i=a^2\left(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}\right)=2a^2\) 

(Đẳng thức quen thuộc \(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}=2\))

Cho \(S_n=8\) \(\Rightarrow2a^2=8\Leftrightarrow a=2\).

Vậy \(a=2\) thỏa mãn ycbt.

có làm thì mới có ăn

BN VÔ TL CÂU HỎI CỦA MIK NHÉ

a)SABC = 1/3 SADC VÌ 

AB = 1/3 CD

CHIỀU CAO HẠ TỪ C XUỐNG AB BẰNG CHIỀU CAO HẠ TỪ A  XUỐNG CD (đều bằng chều cao hình thang ABCD)

b)MÀ HAI TAM GIÁC NAY CHUNG ĐÁY AC NÊN CHIỀU CAO HẠ TỪ B XUỐNG AC BẰNG 1/3

CHIỀU CAO HẠ TỪ D XUÔNG AC

SAOB = 1/3 SAOD VÌ

CHUNG ĐÁY AO

CHIỀU CAO HẠ TỪ B XUÔNG AO BẰNG 1/3 CHIỀU CAO HẠ TỪ D XUỐNG AO

SUY RA SAOD = 3/4 SABC

SABC= 4,5 : 1/3 = 13,5 CM2

SABC = 1/3 SACD ( cmt )

SACD= 13,5 : 1/3 = 40,5 CM2

a: ABCD là hình vuông

=>AB=BC=CD=DA và \(\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{ADC}=90^0\) và AC là phân giác của \(\widehat{DAB}\) và DB là phân giác của góc ADC; BD là phân giác của góc ABC

AC là phân giác của góc DAB

=>\(\widehat{CAB}=\dfrac{1}{2}\widehat{DAB}=\dfrac{1}{2}\cdot90^0=45^0\)

AEBF là hình vuông

=>AB là phân giác của \(\widehat{FAE}\) và \(\widehat{FAE}=90^0\) 

=>\(\widehat{BAE}=\dfrac{1}{2}\cdot\widehat{EAF}=45^0\)

\(\widehat{BAE}=45^0\)

\(\widehat{BAC}=45^0\)

Do đó: \(\widehat{BAE}=\widehat{BAC}=45^0\)

=>AE và AC là hai tia trùng nhau

=>A,E,C thẳng hàng

BD là phân giác của góc ABC

=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)

AEBF là hình vuông

=>BA là phân giác của góc EBF

=>\(\widehat{ABE}=\dfrac{1}{2}\cdot\widehat{FBE}=45^0\)

=>\(\widehat{ABE}=\widehat{ABD}\)

=>BE,BD là hai tia trùng nhau

=>B,E,D thẳng hàng

B,E,D thẳng hàng

A,E,C thẳng hàng

Do đó: BD cắt AC tại E

ADCB là hình vuông

=>AC=BD và AC vuông góc với BD tại trung điểm của mỗi đường

=>AC vuông góc BD tại E và E là trung điểm chung của AC và DB

E là trung điểm của AC nên AC=2AE=2(cm)

E là trung điểm của BD nên BD=2EB=2(cm)

Xét tứ giác ADCB có DB\(\perp\)AC

nên \(S_{ADCB}=\dfrac{1}{2}\cdot DB\cdot AC=\dfrac{1}{2}\cdot2\cdot2=2\left(cm^2\right)\)

b: ADCB là hình vuông

=>\(S_{ADCB}=AB^2\)

=>\(AB^2=2\)

=>\(AB=\sqrt{2}\left(cm\right)\)