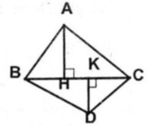
Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S 1 ,  S 2 ,  S 3 . Ta có:

S =  S 1  +  S 2  +  S 3

Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB

S 1  = 1/2 MT. AB

S 2  = 1/2 MK. AC

S 3  = 1/2 MH. BC

a

b

c

d

ĐÃ VẼ LẠI 2 LẦN.LẦN NÀY LÀ LẦN 3

=> CUỘC ĐỜI ĐEN NHỌ CỦA COOL KID :V

a) Ta có:

\(\left\{{}\begin{matrix}BH\perp AC\\KC\perp AC\end{matrix}\right.\)       ⇒ \(BH\text{//}KC\) 

\(\left\{{}\begin{matrix}CH\perp AB\\BK\perp AB\end{matrix}\right.\)       ⇒ \(CH\text{//}BK\)

\(Xét\) \(tứ\) \(giác\) \(BKCH\) \(có:\) \(\left\{{}\begin{matrix}BH\text{//}KC\\CH\text{//}BK\end{matrix}\right.\)

⇒ Tứ giác \(BKCH\) là hình hình hành. Mà M là trung điểm của đường chéo BC

⇒ \(\left\{{}\begin{matrix}H,M,K_{ }thẳng_{ }hàng\\HM=MK\end{matrix}\right.\)

Xét \(\Delta AHK\) có: \(\left\{{}\begin{matrix}AI=IK\left(gt\right)\\HM=MK\left(cmt\right)\end{matrix}\right.\)

⇒ \(IM\) là đường trung bình của \(\Delta AHK\)

⇒ \(IM=\dfrac{1}{2}AH\)              \(\left(ĐPCM\right)\)

c)

Ta có:

\(\dfrac{S_{\Delta HBC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HD.BC}{\dfrac{1}{2}.AD.BC}=\dfrac{HD}{AD}\)  

\(\dfrac{S_{\Delta HAC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HE.AC}{\dfrac{1}{2}.BE.AC}=\dfrac{HE}{BE}\)

\(\dfrac{S_{\Delta HBA}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HF.AB}{\dfrac{1}{2}.CF.AB}=\dfrac{HF}{CF}\)

⇒ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{\Delta HBC}+S_{\Delta HAC}+S_{\Delta HAB}}{S_{\Delta ABC}}=\dfrac{S_{\Delta ABC}}{S_{\Delta ABC}}\)

⇔ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\)          \(\left(ĐPCM\right)\)

a, ^BAC + ^BAK = 180 (kề bù)

^BAC = 135 (gt)

=> ^BAK = 45

xét ΔAKB có : ^AKB = 90

=> ΔAKB vuông cân  (dấu hiệu)

b, ^KBC = 90 - ^KCB 

^CAH = 90 - ^ACH 

=> ^CAH = ^ABK 

^CAH = ^KAE (đối đỉnh)

=> ^ABK = ^KAE 

xét ΔAKE và ΔBKC có : ^CKB = ^AKE = 90

AK = KB do ΔAKB cân tại K (câu a)

=> ΔAKE = ΔBKC (cgv-gnk)

=> AE = BC (định nghĩa)

c, kẻ MK

xét ΔMNE và ΔMNK có : MN chung

^MNE = ^MNK = 90 

NE = NK do N là trung điểm của EK (Gt)

=> ΔMNE = ΔMNK (2cgv)

=> MN = MK (định nghĩa)                                            (1)

      ^EMN = ^KMN (định nghĩa)                                     (2)

MN ⊥ BE ; CK ⊥ BE => MN // CK (định lí)

=> ^EMN = MCK (đồng vị)

     ^NMK = ^MKC (so le trong)

và (2)

=> ^MCK = ^MKC 

=> ΔMKC cân tại M (dấu hiệu)

=> MK = MC (định nghĩa)   và (1)

=> ME = MC mà M nằm giữa C và E

=> M là trung điểm của EC