Cho tanα + cotα = m, hãy tính theo m
tan 3 α + c o t 3 α
Cho góc α thỏa mãn π 2 < α < π và tan α – cotα = 1. Tính P = tanα + cotα
A. P = 1
B. P = -1
C. P = - 5
D. P = 5
Chọn C.
Ta có tan α – cotα = 1

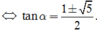
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
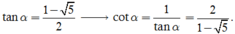
Thay
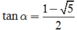 và
và 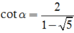
vào P ta được
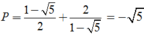
Từ ý nghĩa hình học của tanα và cotα hãy suy ra với mọi số nguyên k, tan(α + kπ) = tanα, cot(α + kπ) = cotα.
Trên đường tròn lượng giác,từ A(1,0) vẽ tiếp tuyến t’At với đường tròn lượng giác.
Từ B(0,1) vẽ tiếp tuyến s’Bs với đường tròn lượng giác .
Cho cung lượng giác AM có số đo α (α ≠ π/2 + kπ ). Gọi T là giao điểm của OM với trục t’At.
Gọi S là giao điểm của OM và trục s’Bs.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm T trên trục tan. Do đó
tan(α + kπ) = tanα.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm S trên trục cot. Do đó
cot(α + kπ) = cotα.
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Nêu định nghĩa của tanα , cotα và giải thích vì sao ta có:
tan(α + kπ) = tanα, k ∈Z;
cot(α + kπ) = cotα, k ∈Z;
cho sin α bằng 1/3 và π/2 <α<π . Tính giá trị của cosα,tanα,và cotα
Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!
Cho cos α = 2/3. Tính giá trị của biểu thức A = tan α + 3 c o t α tan α + c o t α
A. 7/18
B. 1/2
C. 5/12
D. 17/9
Cho cos α=-2/5 và π<α<3π/2. tính tanα, sinα ,cotα
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\dfrac{\sqrt{21}}{5}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\dfrac{\sqrt{21}}{5}}{-\dfrac{2}{5}}=\dfrac{\sqrt{21}}{2}\)
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{2}{\sqrt{21}}\)
Cho góc α thỏa mãn tanα + cotα = 5.Tính P = tan3α + cot3α
A. 98
B. 110
C. 112
D. 114
Chọn B.
Ta có P = tan3α + cot3α = (tanα + cotα) 3 - 3tanα.cotα( tanα + cotα)
= 53 - 3.5 = 110
Cho α là góc nhọn, sinα = 1/2.Tính cosα;tanα;cotα
Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
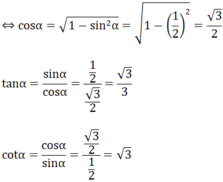
sinα = 2, tanα = 2, cotα = 2 biết cosα = \(\dfrac{1}{3}\) α∈ (0;\(\dfrac{\pi}{2}\))
Tính cosα
$\sin \alpha =2$?? $\sin \alpha \in [-1;1]$ với mọi $\alpha$ mà bạn. Bạn xem lại đề.