Họ nguyên hàm của hàm số f(x)=xcos2x là
A. x sin 2 x 2 − c o s 2 x 4 + C
B. x sin 2 x − c o s 2 x 2 + C
C. x sin 2 x + c o s 2 x 4 + C
D. x sin 2 x 2 + c o s 2 x 4 + C
Một nguyên hàm F(x) của hàm số f x = x cos 2 x thỏa mãn F π = 2017 . Khi đó F(x) là hàm số nào dưới đây?
A. F(x) = xtanx + ln|cosx| + 2017.
B. F(x) = xtanx – ln|cosx| + 2018.
C. F(x) = xtanx + ln|cosx| + 2016.
D. F(x) = xtanx – ln|cosx| + 2017.
Chọn A.
Đặt u=x, d v = 1 cos 2 x d x ta được du = dx, v = tanx
Do đó
F ( x ) = ∫ x cos 2 x d x = x tan x - ∫ tan x d x = x tan x + ln cos x + C
Vì F π = 2017 nên C = 2017. Vậy F(x) = xtanx + ln|cosx| + 2017.
Tìm họ nguyên hàm của hàm số :
\(f\left(x\right)=\frac{5\sin x}{2\sin x-\cos x+1}\)
Biến đổi :
\(5\sin x=a\left(2\sin x-\cos x+1\right)+b\left(2\cos x+\sin x\right)+c\)
= \(\left(2a+b\right)\sin x+\left(2b-a\right)\cos x+a+c\)
Đồng nhất hệ số hai tử số :
\(\begin{cases}2a+b=5\\2b-a=0\\a+c=0\end{cases}\)
\(\Rightarrow\) \(\begin{cases}a=2\\b=1\\c=-2\end{cases}\)
Khi đó :
\(f\left(x\right)=\frac{2\left(2\sin x-\cos x+1\right)+\left(2\cos x+\sin x\right)-2}{2\sin x-\cos x+1}\)
= \(2+\frac{2\cos x+\sin x}{2\sin x-\cos x+1}-\frac{2}{2\sin x-\cos x+1}\)
Do vậy :
\(I=2\int dx+\int\frac{\left(2\cos x+\sin x\right)dx}{2\sin x-\cos x+1}-2\int\frac{dx}{2\sin x-\cos x+1}\)
=\(2x+\ln\left|2\sin x-\cos x+1\right|-2J+C\)
Với
\(J=\int\frac{dx}{2\sin x-\cos x+1}\)
Họ nguyên hàm của hàm số \(f\left(x\right)=sin^2x.cos^2x\) là
\(\int sin^2x.cos^2xdx=\dfrac{1}{4}\int sin^22xdx=\dfrac{1}{8}\int\left(1-cos4x\right)dx\)
\(=\dfrac{1}{8}x-\dfrac{1}{32}sin4x+C\)
Cho y = x cos 2 x trên - π 2 ; π 2 và F(x) là một nguyên hàm của hàm số xf ‘(x) thỏa mãn F(0) = 0. Biết a ∈ - π 2 ; π 2 thỏa mãn tan a = 3. Tính F(a) – 10a2 + 3a
A. 1 2 ln 10
B. - 1 4 ln 10
C. - 1 2 ln 10
D. ln 10
Đáp án A
Phương pháp: Sử dụng phương pháp tích phân từng phần tính F(x)
Cách giải:
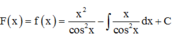
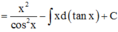
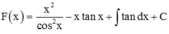
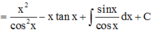

![]()
![]()
=> 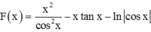
![]()
![]()
![]()
![]()
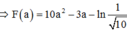
![]()
![]()
Tìm họ nguyên hàm của hàm số lượng giác sau :
\(f\left(x\right)=\int\frac{4\sin x+3\cos x}{\sin x+2\cos x}dx\)
Biến đổi :
\(4\sin x+3\cos x=A\left(\sin x+2\cos x\right)+B\left(\cos x-2\sin x\right)=\left(A-2B\right)\sin x+\left(2A+B\right)\cos x\)
Đồng nhất hệ số hai tử số, ta có :
\(\begin{cases}A-2B=4\\2A+B=3\end{cases}\)\(\Leftrightarrow\begin{cases}A=2\\B=-1\end{cases}\)
Khi đó \(f\left(x\right)=\frac{2\left(\left(\sin x+2\cos x\right)\right)-\left(\left(\sin x-2\cos x\right)\right)}{\left(\sin x+2\cos x\right)}=2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\)
Do đó,
\(F\left(x\right)=\int f\left(x\right)dx=\int\left(2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\right)dx=2\int dx-\int\frac{\left(\cos x-2\sin x\right)dx}{\sin x+2\cos x}=2x-\ln\left|\sin x+2\cos x\right|+C\)
Tìm họ nguyên hàm của hàm số
\(f\left(x\right)=\frac{2}{\sqrt{3}\sin x+\cos x}\)
Ta có :
\(f\left(x\right)=\int\frac{dx}{\sqrt{3}\sin x+\cos x}=\frac{1}{2}\int\frac{dx}{\frac{\sqrt{3}}{2}\sin x+\frac{1}{2}\cos x}=\frac{1}{2}\int\frac{dx}{\sin\left(x+\frac{\pi}{6}\right)}\)
\(=\int\frac{dx}{2\tan\left(\frac{x}{2}+\frac{\pi}{12}\right)\cos^2\left(\frac{x}{2}+\frac{\pi}{12}\right)}=\int\frac{dx}{\sin\left(\frac{x}{2}+\frac{\pi}{12}\right)\cos\left(\frac{x}{2}+\frac{\pi}{12}\right)}=\int\frac{d\left(\tan\frac{x}{2}+\frac{\pi}{12}\right)}{\tan\left(\frac{x}{2}+\frac{\pi}{12}\right)}=\ln\left|\tan\left(\frac{x}{2}+\frac{\pi}{12}\right)\right|+C\)
Tìm họ nguyên hàm của hàm số lượng giác :
\(f\left(x\right)=\frac{1}{2\sin x+1}\)
Biến đổi f(x) về dạng :
\(f\left(x\right)=\frac{1}{2\left(\sin x+\frac{1}{2}\right)}=\frac{1}{2}\frac{1}{\sin x+\sin\frac{\pi}{6}}=\frac{1}{4}\frac{1}{\sin\frac{6x+\pi}{12}.\cos\frac{6x-\pi}{12}}\left(1\right)\)
Sử dụng đồng nhất thức :
\(1=\frac{\cos\frac{\pi}{6}}{\cos\frac{\pi}{6}}=\frac{\cos\left[\frac{6x+\pi}{12}-\frac{6x-\pi}{12}\right]}{\frac{\sqrt{3}}{2}}+\frac{2}{\sqrt{3}}\frac{\cos\left(\frac{6x+\pi}{12}\right).\cos\left(\frac{6x-\pi}{12}\right)+\sin\left(\frac{6x+\pi}{12}\right).\sin\left(\frac{6x-\pi}{12}\right)}{\sin\left(\frac{6x+\pi}{12}\right).\cos\left(\frac{6x-\pi}{12}\right)}\)
Ta được :
\(f\left(x\right)=\frac{2}{\sqrt{3}}\left[\int\frac{\cos\left(\frac{6x+\pi}{12}\right)}{\sin\left(\frac{6x+\pi}{12}\right)}dx-\int\frac{\sin\left(\frac{6x-\pi}{12}\right)}{\cos\left(\frac{6x-\pi}{12}\right)}\right]=\frac{2}{\sqrt{3}}\left(\ln\left|\sin\right|\left(\frac{6x+\pi}{12}\right)-\ln\left|\cos\right|\left(\frac{6x-\pi}{12}\right)\right)\)
\(=\frac{2}{\sqrt{3}}\ln\left|\frac{\sin\left(\frac{6x+\pi}{12}\right)}{\cos\left(\frac{6x-\pi}{12}\right)}\right|+C\)
Nguyên hàm của hàm số f ( x ) = sin x . 2 − cos x là
A. F ( x ) = 2 3 ( 2 − cos x ) 2 − cos x + C
B. F ( x ) = − 3 2 ( 2 − cos x ) 2 − cos x + C
C. F ( x ) = − 1 2 2 − cos x + C
D. F ( x ) = 2 3 2 − cos x + C
Tìm họ nguyên hàm của hàm số :
\(f\left(x\right)=\frac{4\sin^2x+1}{\sqrt{3}\sin x+\cos x}\)
Biến đổi :
\(4\sin^2x+1=5\sin^2x+\cos^2x=\left(a\sin x+b\cos x\right)\left(\sqrt{3}\sin x+\cos x\right)+c\left(\sin^2x+\cos^2x\right)\)
\(=\left(a\sqrt{3}+c\right)\sin^2x+\left(a+b\sqrt{3}\right)\sin x.\cos x+\left(b+c\right)\cos^2x\)
Đồng nhấtheej số hai tử số
\(\begin{cases}a\sqrt{3}+c=5\\a+b\sqrt{3}=0\\b+c=1\end{cases}\)
\(\Leftrightarrow\) \(\begin{cases}a=\sqrt{3}\\b=-1\\c=2\end{cases}\)