Chọn A.
Đặt u=x, d v = 1 cos 2 x d x ta được du = dx, v = tanx
Do đó
F ( x ) = ∫ x cos 2 x d x = x tan x - ∫ tan x d x = x tan x + ln cos x + C
Vì F π = 2017 nên C = 2017. Vậy F(x) = xtanx + ln|cosx| + 2017.
Chọn A.
Đặt u=x, d v = 1 cos 2 x d x ta được du = dx, v = tanx
Do đó
F ( x ) = ∫ x cos 2 x d x = x tan x - ∫ tan x d x = x tan x + ln cos x + C
Vì F π = 2017 nên C = 2017. Vậy F(x) = xtanx + ln|cosx| + 2017.
Cho hàm số f(x) thỏa mãn f'(x)=27+cosx và f(0)=2019. Mệnh đề nào dưới đây đúng?
![]()
![]()
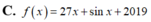
![]()
Tìm nguyên hàm F(x) của hàm số f(x)=sinx+cosx thỏa mãn F π 2 = 2
A. F (x)= -cosx +sinx+1
B. F (x)= -cosx+sinx-1
C. F(x)= cosx-sinx +3
D. F (x)= -cosx+sinx +3
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số
A. f ( x ) = sin x + cos x sin x - cos x
B. f ( x ) = sin x - cos x sin x + cos x
C. f ( x ) = 1 sin x + cos x
D. f ( x ) = 1 sin x - cos x
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F(0) = –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) = 3.
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = sin 3 x . cos x . Tính I = F π 2 - F ( 0 )
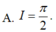
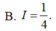
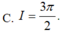
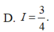
Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = ln 2 x + 1 . ln x x thoả mãn F ( 1 ) = 1 3 . Giá trị của F 2 ( e ) là
A. 8 9
B. 1 9
C. 8 3
D. 1 3
Biết F(x) là một nguyên hàm của hàm số f(x) = sin 2x + cosx. Giá trị F π 2 - F ( 0 ) bằng
A. 2.
B. 1.
C. -1.
D. 4.
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
Họ nguyên hàm của hàm số f ( x ) = e x + cos x + 2018 là
![]()
![]()
![]()
![]()