Trong các hàm số sau đây, hàm số nào đồng biến trên R
A. y = π 3 x
B. y = 1 3 x
C. y = 2 e x
D. y = 1 2 x
cho hàm số y= x3. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(R\)
B. Hàm số đồng biến trên \(R\)
C. Hàm số đồng biến trên (-∞;0)
D. Hàm số nghịch biến trên (0;+∞)
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y = f ' x như hình bên dưới
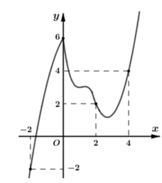
Hàm số g x = 2 f x − x 2 đồng biến trên khoảng nào trong các khoảng sau đây?
A. 2 ; + ∞ .
B. − ∞ ; − 2 .
C. (-2;2)
D. (2;4)
Cho hàm số y= f( x) có đạo hàm liên tục trên R. Đồ thị hàm số y= f’(x) như hình bên dưới
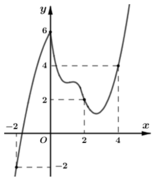
Hàm số g(x) = 2 . f(x) – x2 đồng biến trên khoảng nào trong các khoảng sau đây?
A. ( - ∞ ; - 2 )
B. (-2; 2)
C. (2; 4)
D. ( 2 ; + ∞ )
Khẳng định nào sau đây đúng?
A. y = sin3x là hàm số chẵn
B. Hàm số 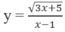 xác định trên R
xác định trên R
C. Hàm số y = x 3 + 4x - 5 đồng biến trên R
D. Hàm số y = sinx + 3x - 1 nghịch biến trên R
Khẳng định nào sau đây đúng?
A. y = sin3x là hàm số chẵn
B. Hàm số y = 3 x + 5 x - 1 xác định trên R
C. Hàm số y = x 3 + 4x - 5 đồng biến trên R
D. Hàm số y = sinx + 3x - 1 nghịch biến trên R
Đáp án: C.
Vì y' = 3 x 2 + 4 > 0, ∀ x ∈ R.
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
\(\left(\frac{2x-1}{x+2}\right)'=\frac{5}{\left(x+2\right)^2}>0\)
Vậy hàm số \(y=\frac{2x-1}{x+2}\) đồng biến trên R. Chọn A.
A. là hàm phân thức bậc nhất trên bậc nhất nên không đồng biến trên \(ℝ\).
B., D. là đa thức, có hệ số cao nhất âm nên cũng không thể đồng biến trên \(ℝ\).
C>: \(\left(x^3+2x+1\right)'=3x^2+2>0,\forall x\inℝ\).
Ta chọn C.
Cho hàm số y = x3 + 3x2 – 9x – 7 . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-3;1) .
B. Hàm số đồng biến trên (-9;-5).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (5;+∞).
Tập xác định: D = R.
Ta có: 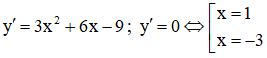
Bảng biến thiên:
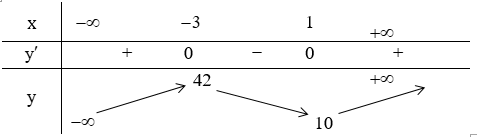
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;-3),(1;+∞) . Hàm số nghịch biến trên khoảng (-3;1)
Chọn C.
Cho hàm số y = f(x) xác định trên R, có bảng biến thiên sau
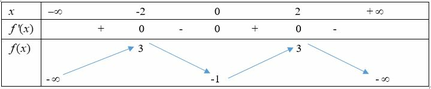
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A. (0;2)
B. (-1;3)
C. (- ∞ ;3)
D. (- ∞ ;0)
Cho hàm số y = f x liên tục trên R và có bảng biến thiên như hình dưới đây. Bao nhiêu mệnh đề sai trong các mệnh đề sau đây?
I. Hàm số đồng biến trên các khoảng - ∞ ; - 5 và ( - 3 ; - 2 ] .
II. Hàm số đồng biến trên khoảng - ∞ ; 5 .
III. Hàm số nghịch biến trên khoảng - 2 ; + ∞ .
IV. Hàm số đồng biến trên khoảng ( - ∞ ; - 2 ] .
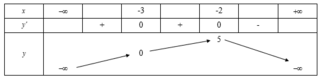
A. 1
B. 2
C. 3
D. 4
Trong các hàm số sau, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của hàm số đó? Vì sao?
a) \(y = {\left( {\frac{{\sqrt 3 }}{2}} \right)^x}\)
b) \(y = {\left( {\frac{{\sqrt[3]{{26}}}}{3}} \right)^x}\)
c) \(y = {\log _\pi }x\)
d) \(y = {\log _{\frac{{\sqrt {15} }}{4}}}x\)
\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)