Hàm số nào sau đây không đồng biến trên khoảng − ∞ ; + ∞ ?
A. y = x − 2 x − 1
B. y = x 5 + x 3 − 10
C. y = x 3 + 1
D. y = x + 1
Hàm số nào sau đây không đồng biến trên khoảng - ∞ ; + ∞ ?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Hàm số nào sau đây không đồng biến trên khoảng − ∞ , + ∞
A. y = x − 1 x + 2
B. y = x 3 + 2
C. y = x + 1
D. y = x 5 + x 3 − 1
Đáp án A
Phương Pháp: Tính giới hạn từng hàm số trên khoảng − ∞ , + ∞
Hàm số nào sau đây không đồng biến trên khoảng (-∞;+∞)
A. y = x - 1 x + 2
B. y = x 3 + 2
C. y = x + 1
D. y = x 5 + x 3 - 1
Đáp án A
Phương pháp:
* Phương pháp xét sự đồng biến, nghịch biến của các hàm số:
- Bước 1: Tìm tập xác định, tính f'(x)
- Bước 2: Tìm các điểm tại đó f'(x) = 0 hoặc f'(x) không xác định
- Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên
- Bước 4: Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Cách giải:
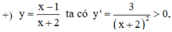
![]()
=> Hàm số đồng biến trên các khoảng (-∞;-2);(-2;+∞)
+) y = x3 + 2 ⇒ y'= 3x2 ≥ 0,∀ x∈R: Hàm số đồng biến trên R.
+) y = x + 1 ⇒ y' = 1 > 0, ∀ x∈R: Hàm số đồng biến trên R.
+) y = x5 + x3 - 1 ⇒ y' = 5x4 + 3x2 ≥ 0, ∀ x ∈ R; y' = 0 ⇔ x = 0 ⇒ Hàm số đồng biến trên R.
Cho hàm số:
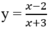
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Cho hàm số y = x3 + 3x2 – 9x – 7 . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-3;1) .
B. Hàm số đồng biến trên (-9;-5).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (5;+∞).
Tập xác định: D = R.
Ta có: 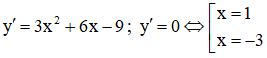
Bảng biến thiên:
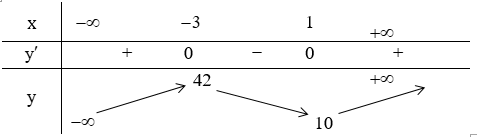
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;-3),(1;+∞) . Hàm số nghịch biến trên khoảng (-3;1)
Chọn C.
Hàm số nào trong các hàm số sau đây đồng biến trên khoảng (1;3)?
A. y = 4 − x 2
B. y = x 4 − 2 x 2 − 1
C. y = e − x
D. y = x + 1 2 x − 3
Cho hàm số . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-∞;-1)
B. Hàm số nghịch biến trên khoảng (-1;\(\dfrac{1}{2}\))
C. Hàm số đồng biến trên mỗi khoảng (-∞;-1) và (\(\dfrac{1}{2}\);+∞)
D. Hàm số nghịch biến trên khoảng (-1;\(\dfrac{1}{2}\))và đồng biến trên khoảng(\(\dfrac{1}{2}\);+∞)