Cho a là số thực dương khác 1. Tính I = log a a .
A. I = -2
B. I = 0
C. I = 1 2 .
D. I = 2
Cho a là số thực dương khác 1. Tính I = log a a
A. I = 1 2
B. I = 0
C. I = -2
D. I = 2
Cho a là số thực dương khác 1. Tính I = log a a .
A. I = 1 2
B. I = - 1 2
C. I = -2
D. I = 2
Bài 1: Cho a > 0, b > 0. Chứng minh rằng:
a/√b + b/√a >= √a + √b
Bài 2: Cho a, b, c là các đô dài của các cạnh tam giác và p là nửa chu vi. Chứng minh rằng:
(p - a)(p - b) <= c^2/4
Bài 3:Chứng minh rằng với mọi số thực a ta có:3(a^4+a^2+1)>=(a^2+a+1)^2
Bài 4:Cho 3 số thực dương a,b,c.chứng minh rằng:(1+a/b)(1+b/c)(1+c/a)>=8
Bài 5:Cho a,b là hai số dương. Chứng minh:a^2+b^2+1/a++1/b>=2(√a+√b)
Bài 6:Cho ba số dương a,b,c. Chứng minh rằng:ab/(a+b)+bc/(b+c)+ca/(c+a)<=(a+b+c)/2
Bài 7:Cho ba số thực dương a,b,c thỏa mãn:ab+bc+ca=3. Chứng minh rằng:
a^3/(b^2+3)+b^3/(c^2+3)+c^3/(a^2+3)>=3/4
bài 8:Tìm giá trị nhỏ nhất của hàm số f(x)=x+3/(x-2) với x>2
Bài 6 . Áp dụng BĐT Cauchy , ta có :
a2 + b2 ≥ 2ab ( a > 0 ; b > 0)
⇔ ( a + b)2 ≥ 4ab
⇔ \(\dfrac{\left(a+b\right)^2}{4}\)≥ ab
⇔ \(\dfrac{a+b}{4}\) ≥ \(\dfrac{ab}{a+b}\) ( 1 )
CMTT , ta cũng được : \(\dfrac{b+c}{4}\) ≥ \(\dfrac{bc}{b+c}\) ( 2) ; \(\dfrac{a+c}{4}\) ≥ \(\dfrac{ac}{a+c}\)( 3)
Cộng từng vế của ( 1 ; 2 ; 3 ) , Ta có :
\(\dfrac{a+b}{4}\) + \(\dfrac{b+c}{4}\) + \(\dfrac{a+c}{4}\) ≥ \(\dfrac{ab}{a+b}\) + \(\dfrac{bc}{b+c}\) + \(\dfrac{ac}{a+c}\)
⇔ \(\dfrac{a+b+c}{2}\) ≥ \(\dfrac{ab}{a+b}\) + \(\dfrac{bc}{b+c}\) + \(\dfrac{ac}{a+c}\)
Bài 4.
Áp dụng BĐT Cauchy cho các số dương a , b, c , ta có :
\(1+\dfrac{a}{b}\) ≥ \(2\sqrt{\dfrac{a}{b}}\) ( a > 0 ; b > 0) ( 1)
\(1+\dfrac{b}{c}\) ≥ \(2\sqrt{\dfrac{b}{c}}\) ( b > 0 ; c > 0) ( 2)
\(1+\dfrac{c}{a}\) ≥ \(2\sqrt{\dfrac{c}{a}}\) ( a > 0 ; c > 0) ( 3)
Nhân từng vế của ( 1 ; 2 ; 3) , ta được :
\(\left(1+\dfrac{a}{b}\right)\left(1+\dfrac{b}{c}\right)\left(1+\dfrac{c}{a}\right)\) ≥ \(8\sqrt{\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{a}}=8\)
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
I 3 a = 2 ⇔ a = log 3 2 I I ∀ x ∈ ℝ \ 0 , log 2 x 2 = 2 log 2 x I I I log a b c = log a b . log a c
Trong ba mệnh đề I , I I , I I I số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho a là số thực dương khác 2 .Tính I = log a 2 a 2 2 .
A. I = 2
B. I = - 1 2
C. I = - 2
D. I = 1 2
Cho a là số thực dương khác 2. Tính I = log a 2 ( a 2 4 )
A. I = 1 2
B. I = 2
C. I = - 1 2
D. I = -2
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
( I ) 3 a = 2 ⇔ a = log 3 2
( II ) ∀ x ∈ R \ { 0 } , log 2 x 2 = 2 log 2 x
( III ) log a ( bc ) = log a b . log a c
Trong ba mệnh đề (I), (II), (III) số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
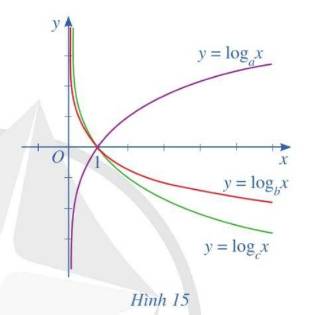
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.