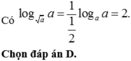Các câu hỏi tương tự
Cho a là số thực dương khác 2 .Tính
I
log
a
2
a
2
2
. A.
I
2
B.
I
-
1
2
C.
I
-
2
D.
I
1
2
Đọc tiếp
Cho a là số thực dương khác 2 .Tính I = log a 2 a 2 2 .
A. I = 2
B. I = - 1 2
C. I = - 2
D. I = 1 2
Cho a là số thực dương khác 1. Tính I = log a a .
A. I = -2
B. I = 0
C. I = 1 2 .
D. I = 2
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau
I
3
a
2
⇔
a
log
3
2
I
I
∀
x
∈
ℝ
0
,
log
2
x
2...
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
I 3 a = 2 ⇔ a = log 3 2 I I ∀ x ∈ ℝ \ 0 , log 2 x 2 = 2 log 2 x I I I log a b c = log a b . log a c
Trong ba mệnh đề I , I I , I I I số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho số phức z thỏa mãn |z - 1 + 3i|+|z + 5 + i| 2
65
Giá trị nhỏ nhất của |z + 2 + i| đạt được khi z a + bi với a,b là các số thực dương. Giá trị của
2
a
2
+
b
2
bằng A. 17 B. 33 C. 24 D. 36
Đọc tiếp
Cho số phức z thỏa mãn
|z - 1 + 3i|+|z + 5 + i| = 2 65 Giá trị nhỏ nhất của
|z + 2 + i| đạt được khi z = a + bi với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
A. 17
B. 33
C. 24
D. 36
Cho số phức z thỏa mãn
z
-
1
+
3
i
+
z
¯
+
5
+
i
2
65
. Giá trị nhỏ nhất của
z
+
2
+
i...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 . Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a, b là các số thực dương. Giá trị của 2 b + 3 a bằng
A. 19
B. 16
C. 24
D. 13
Cho a là số thực dương khác 5. Tính
I
log
a
5
a
3
125
A.
I
-
1
3
B. I -3 C.
I
1
3
D. I 3
Đọc tiếp
Cho a là số thực dương khác 5. Tính I = log a 5 a 3 125
A. I = - 1 3
B. I = -3
C. I = 1 3
D. I = 3
Cho số phức za+bi
a
,
b
∈
R
thỏa mãn
z
5
và
z
(
2
+
i
)
(
1
-
2
i
)
là một số thực. Tính
P
a
+
b...
Đọc tiếp
Cho số phức z=a+bi a , b ∈ R thỏa mãn z = 5 và z ( 2 + i ) ( 1 - 2 i ) là một số thực. Tính P = a + b .
A. P=5
B. P=7
C. P=8
D. P=4
Cho tích phân
I
∫
0
a
x
e
x
d
x
, với a là số thực dương. Tìm a để
I
1
. A.
a
1
. B.
a
e
. C.
a
0
. D.
a
2
.
Đọc tiếp
Cho tích phân I = ∫ 0 a x e x d x , với a là số thực dương. Tìm a để I = 1 .
A. a = 1 .
B. a = e .
C. a = 0 .
D. a = 2 .
Cho a là một số thực dương. Tính
I
∫
0
a
l
x
(
x
+
1
)
d
x
A.
I
l
a
a
B.
I
l
a
C.
I
l
a
(...
Đọc tiếp
Cho a là một số thực dương. Tính I = ∫ 0 a l x ( x + 1 ) d x
A. I = l a a
B. I = l a
C. I = l a ( a - 1 )
D. I = l a ( a + 1 )