
Những câu hỏi liên quan
Cho đường tròn (O; R) và B nằm trên (O). Từ điểm A bất kì nằm trên tiếp tuyến d tại B với (O), kẻ BH
⊥
AO tại Ha, Khi A di chuyến trên d, chứng minh tích OH.OA có giá trị không đổib, Gọi C là điểm đối xứng của B qua H. Chứng minh AC là tiếp tuyến của (O)c, Tia đối của tia OA cắt (O) tại M. Chứng minh M cách đều ba đường thẳng BC, AB, AC
Đọc tiếp
Cho đường tròn (O; R) và B nằm trên (O). Từ điểm A bất kì nằm trên tiếp tuyến d tại B với (O), kẻ BH ⊥ AO tại H
a, Khi A di chuyến trên d, chứng minh tích OH.OA có giá trị không đổi
b, Gọi C là điểm đối xứng của B qua H. Chứng minh AC là tiếp tuyến của (O)
c, Tia đối của tia OA cắt (O) tại M. Chứng minh M cách đều ba đường thẳng BC, AB, AC
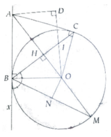
a, OH.OA = O B 2 = R 2 không đổi\
b, Chứng minh ∆ABO = ∆ACO
c, Vẽ ON ⊥ BM => B O N ^ = M O N ^
có B O N ^ = M B x ^ ; M O N ^ = H B M ^
=> M B x ^ = H B M ^
=> MB là phân giác của
C
B
x
^
nên M cách đều hai cạnh BA và BC mà AM là phân giác
B
A
C
^
=> đpcm
d, Ta có ∆ODA:∆OHI => OI.OD = OH.OA = R 2
Ta có: 3OI+OD ≥ 2 3 O I . O D = 2R 3
=> (3OI+OD)min = 2R 3 <=> OI = R 3 3
Đúng 0
Bình luận (0)
Cho tam giác ABH vuông tại H, góc B = 60 độ. Lấy M bất kì trên BH, kẻ MK vuông góc AB tại K. Gọi O là trung điểm AM. CMR: KOH là tam giác đều.
Cho nửa (O;AB/2) M thuộc nửa (O), H là điểm chính giữa cung AM, BH cắt AM ở I . Tiếp tuyến của (O) tại A cắt BH tại K. Nối AH cắt BM tại E. Tìm vị trí của M để góc MKA =90 độ
Cho tam giác ABH có H=90độ; B=60độ. Lấy M bất kì trên BH, kẻ MK vuông góc AB. Gọi O là trung điểm AM. CMR : Tam giác KHO đều.
Cho tam giác ABC ( gócA=90 độ) , lấy một điểm H bất kì trên cạnh AC , kẻ HM vuông góc BC (M thuộc BC)
a) Chứng minh 4 điểm A,B,M,H cùng thuộc một đường tròn
b) Chứng minh BH>AM
cho nửa đường tròn (O;R) đường kính AB. M thuộc nửa đường tròn. H là điểmc hính giữa cung AM. Nối BH cắt AM tại I. Tiếp tuyến của nửa đường trong tại A cắt BH tại K. Nối AH cắ BM tại E
a, chứng minh BAE là tam giác cân
b, chứng minh KH.KB=KE2
c, tìm vị trí của M để góc MKA=90
Cho tam giác ABC đều, các đường cao AD, BH, CK của tam giác cắt nhau tại O. M là một điểm bất kì trên cạnh BC (M không trung với B, C, D) .Kẻ MP và MQ lần lượt vuông góc với AB và AC. PQ cắt OM tại R. Chứng minh rằng R la trung điểm PQ
Cho đường tròn (O; R). Từ điểm A trên (O), kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điếm M bất kì (M khác A), kẻ cát tuyến MNP, gọi K là trung điểm NP, kẻ tiếp tuyến MB, kẻ AC
⊥
MB, BD
⊥
MA. Gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB. Chứng minh:a, Bốn điểm A, M, B, O cùng thuộc một đường trònb, Năm điểm O, K, A, M, B cùng thuộc một đường trònc, OI.OM
R
2
và OI.IM ...
Đọc tiếp
Cho đường tròn (O; R). Từ điểm A trên (O), kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điếm M bất kì (M khác A), kẻ cát tuyến MNP, gọi K là trung điểm NP, kẻ tiếp tuyến MB, kẻ AC ⊥ MB, BD ⊥ MA. Gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB. Chứng minh:
a, Bốn điểm A, M, B, O cùng thuộc một đường tròn
b, Năm điểm O, K, A, M, B cùng thuộc một đường tròn
c, OI.OM = R 2 và OI.IM = I A 2
d, OAHB là hình thoi
e, O, H, M thẳng hàng
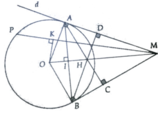
a, HS tự làm
b, Chú ý O K M ^ = 90 0 và kết hợp ý a) => A,M,B,O,K ∈ đường tròn đường kính OM
c, Sử dụng hệ thức lượng trong tam giác vuông OAM ( hoặc có thể chứng minh tam giác đồng dạng)
d, Chứng minh OAHB là hình bình hành và chú ý A,B thuộc (O;R) suy ra OAHB là hình thoi
e, Chứng minh OH ⊥ AB, OMAB => O,H,M thẳng hàng
Đúng 0
Bình luận (0)
tam giác ABC có 3 góc nhọn (AB<AC). M trung điểm AC. Lấy D là trung điểm DB. Chứng minh:
a/ AD=BC
b/ Tam giác ABC = Tam giác CDA
c/ Trên BC lấy H bất kì và AD lấy K bất kì sao cho BH = DK. Chứng minh AH=CK
d/ Chứng minh H,M,K thẳng hàng
Kiểm tra lại đề nhé!:) D là trung điểm DB ?????
Đúng 0
Bình luận (0)














