Question

Cho đường tròn (O; R). Từ điểm A trên (O), kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điếm M bất kì (M khác A), kẻ cát tuyến MNP, gọi K là trung điểm NP, kẻ tiếp tuyến MB, kẻ AC ⊥ MB, BD ⊥ MA. Gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB. Chứng minh:

a, Bốn điểm A, M, B, O cùng thuộc một đường tròn

b, Năm điểm O, K, A, M, B cùng thuộc một đường tròn

c, OI.OM = R 2 và OI.IM =  I A 2

d, OAHB là hình thoi

e, O, H, M thẳng hàng

Answer 1

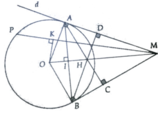
a, HS tự làm

b, Chú ý  O K M ^ = 90 0  và kết hợp ý a) => A,M,B,O,K ∈ đường tròn đường kính OM

c, Sử dụng hệ thức lượng trong tam giác vuông OAM ( hoặc có thể chứng minh tam giác đồng dạng)

d, Chứng minh OAHB là hình bình hành và chú ý A,B thuộc (O;R) suy ra OAHB là hình thoi

e, Chứng minh OH ⊥ AB, OMAB => O,H,M thẳng hàng