Gọi S là tập các giá trị của tham số m để đường thẳng d : y = x + 1 cắt đồ thị hàm số y = 4 x - m 2 x - 1 tại đúng một điểm. Tìm tích các phần tử của S.
A. 5
B. 4
C. 5
D. 20
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng d: y=-x+m cắt đồ thị hàm số y = - 2 x + 1 x + 1 tại hai điểm phân biệt A, B sao cho A B ≤ 2 2 . Tổng giá trị tất cả các phần tử của S bằng
A. -6
B. 0
C. 9
D. -27
Gọi S là tập tất cả các giá trị của tham số m để đường thẳng d : y = x + 1 cắt đồ thị hàm số y = 4 x - m 2 x - 1 tại đúng một điểm. Tích các phần tử của S bằng
A. 5
B. 4
C. 5
D. 20
Cho hàm số y = x^2 + 3x có đồ thị (P). Gọi S là tập hợp các giá trị của tham số m để đường thẳng d : y = x + m^2 cắt đồ thị (P) tại hai điểm phân biệt A,B sao cho trung điểm I của đoạn AB nằm trên đường thẳng d': y= 2x+3. Tổng bình phương các phần tử của S là
Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng d : y = - x + m cắt đồ thị hàm số y = - 2 x + 1 x + 1 tại hai điểm phân biệt A, B sao cho A B ≤ 2 2 . Tổng giá trị tất cả các phần tử của S bằng:
A. -6
B. 0
C. 9
D. -27
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc với đường thẳng d : y = x + 2 Số phần tử của S là
A. 0
B. 1
C. 2
D. 3
Gọi S là tập các giá trị của tham số m để đường thẳng d : y = x + 1 và đồ thị hàm số y = 4 x - m 2 x - 1 có đúng một điểm chung. Tìm tích các phần tử của S.
A. 5
B. 20
C. 4
D. 5
Chọn đáp án B
Phương trình hoành độ giao điểm của đường thẳng d và đồ thị (C):
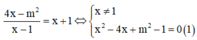
Đường thẳng d và đồ thị (C) có đúng một điểm chung ⇔ Phương trình (1) có đúng 1 nghiệm khác 1

Vậy tích các phần tử của S bằng 20.
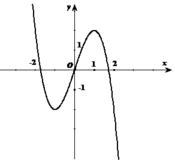
Tập tất cả các giá trị của tham số m để đường thẳng d : y = x + m 2 cắt đồ thị hàm số ( C ) : y = - x 3 + 4 x tại ba điểm phân biệt là
A. (-1;1)
B. ( - ∞ ; 1 ]
C. R
D. - 2 ; 2
Chọn D.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
![]()
Ta khảo sát hàm số (C): y = -x3 + 3x có đồ thị sau như hình bên.
Tìm được ![]() nên yêu cầu bài toán
nên yêu cầu bài toán
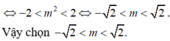
Cho d là đường thẳng đi qua điểm A - 1 ; 3 và có hệ số góc m. Gọi S là tập hợp các giá trị của tham số m để đường thẳng d cắt đồ thị C của hàm số y = x 3 - 3 x + 1 tại ba điểm phân biệt A, B, C sao cho tiếp tuyến với đồ thị tại B và C cắt nhau tại điểm I nằm trên đường tròn đường kính BC. Tính tổng bình phương các phần tử thuộc tập hợp S.
A. 16 9
B. 34 9
C. 38 9
D. 34 3
Chọn đáp án B.

d và (C) cắt nhau tại ba điểm phân biệt

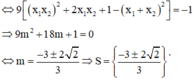
Tổng bình phương các phần tử của S là

Cho hàm số y = 2 x 3 - 3 m 2 - m + 1 x 2 + 6 m 2 - 6 m x , với m là tham số. Gọi S là tập hợp các giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị, đồng thời đường thẳng đi qua hai điểm cực trị đó vuông góc với đường thẳng y = x + 2 . Số phần tử của tập hợp S là
A. 2
B. 3
C. 1
D. 4
Chọn đáp án D
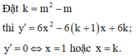
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
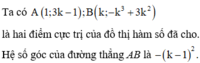
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi
