Các câu hỏi tương tự
Cho hàm số
y
2
x
3
-
3
m
2
-
m
+
1
x
2
+
6
m
2
-
6
m
x
, với m là tham số. Gọi S là t...
Đọc tiếp
Cho hàm số y = 2 x 3 - 3 m 2 - m + 1 x 2 + 6 m 2 - 6 m x , với m là tham số. Gọi S là tập hợp các giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị, đồng thời đường thẳng đi qua hai điểm cực trị đó vuông góc với đường thẳng y = x + 2 . Số phần tử của tập hợp S là
A. 2
B. 3
C. 1
D. 4
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng d: y-x+m cắt đồ thị hàm số
y
-
2
x
+
1
x
+
1
tại hai điểm phân biệt A, B sao cho
A
B
≤
2
2
. Tổng giá trị tất cả các phần tử của S...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng d: y=-x+m cắt đồ thị hàm số y = - 2 x + 1 x + 1 tại hai điểm phân biệt A, B sao cho A B ≤ 2 2 . Tổng giá trị tất cả các phần tử của S bằng
A. -6
B. 0
C. 9
D. -27
Gọi S là tập hợp tất cả các giá trị thực của a sao cho đường thẳng ya(x-1)-3 cắt đồ thị (C) của hàm số
y
2
x
3
-
3
x
2
-
2
tại ba điểm M,N,P(1;-3) và tiếp tuyến của (C) tại M,N vuông góc với nhau. Tổng các phần tử của S bằng A. -1. B. 1. C. 2. D. -2
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của a sao cho đường thẳng y=a(x-1)-3 cắt đồ thị (C) của hàm số y = 2 x 3 - 3 x 2 - 2 tại ba điểm M,N,P(1;-3) và tiếp tuyến của (C) tại M,N vuông góc với nhau. Tổng các phần tử của S bằng
A. -1.
B. 1.
C. 2.
D. -2
Cho hàm số
y
x
3
-
3
x
có đồ thị (C). Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng
d
:
y
k
(
x
+
1
)
+
2
cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M (-1;2), tính tích tất cả các phần tử của tập S A....
Đọc tiếp
Cho hàm số y = x 3 - 3 x có đồ thị (C). Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng d : y = k ( x + 1 ) + 2 cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M (-1;2), tính tích tất cả các phần tử của tập S
A. 1 9
B. - 2 9
C. 1 3
D. -1
(Đề tham khảo của Bộ) Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
y
1
3
x
3
−
m
x
2
+
m
2
−
1
x
có hai điểm cực trị là A và B sao cho A,B nằm khác phía và cách đều đường thẳng
y...
Đọc tiếp
(Đề tham khảo của Bộ) Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 1 3 x 3 − m x 2 + m 2 − 1 x có hai điểm cực trị là A và B sao cho A,B nằm khác phía và cách đều đường thẳng y = 5 x − 9. Tính tổng tất cả các phần tử của S.
A. -1.
B. 0.
C. 1.
D. 2.
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số
y
1
3
x
3
−
m
x
2
+
m
2
−
1
x
có hai điểm cực trị là A và B sao cho A,B nằm khác phía và cách đều đường thẳng
y
5
x...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số y = 1 3 x 3 − m x 2 + m 2 − 1 x có hai điểm cực trị là A và B sao cho A,B nằm khác phía và cách đều đường thẳng y = 5 x − 9 . Tính tích các phần tử của S
A. 3
B. 0
C. 18
D. - 27
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y m cắt đồ thị hàm số y x3 – 3x2 tại 3 điểm phân biệt A, B, C (B nằm giữa A và C) sao cho AB 2BC. Tính tổng các phần tử thuộc S. B. 0 C. -2 D. -4
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số y = x3 – 3x2 tại 3 điểm phân biệt A, B, C (B nằm giữa A và C) sao cho AB = 2BC. Tính tổng các phần tử thuộc S.
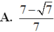
B. 0
C. -2
D. -4
Gọi là tập hợp tất cả các giá trị thực của tham số m để đường thẳng
y
m
cắt đồ thị hàm số
y
x
3
−
3
x
2
tại 3 điểm phân biệt A;B;C (B nằm giữa A và C) sao cho
A
B
2
B
C
. Tính tổng của các phần tử thuộc S. A. -2 B. -4 C. 0 D.
7
−...
Đọc tiếp
Gọi là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số y = x 3 − 3 x 2 tại 3 điểm phân biệt A;B;C (B nằm giữa A và C) sao cho A B = 2 B C . Tính tổng của các phần tử thuộc S.
A. -2
B. -4
C. 0
D. 7 − 7 7
Cho hàm số
y
x
3
-
3
x
có đồ thị (C). Gọi S là tập hợp tất cả các giá thực của k để đường thẳng y k(x+1)+2 cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M(-1;2), tính tích tất cả các phần tử của tập S. A. 1/9 B. -2/9 C. 1/3 D. -1.
Đọc tiếp
Cho hàm số y = x 3 - 3 x có đồ thị (C). Gọi S là tập hợp tất cả các giá thực của k để đường thẳng y = k(x+1)+2 cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M(-1;2), tính tích tất cả các phần tử của tập S.
A. 1/9
B. -2/9
C. 1/3
D. -1.