Các câu hỏi tương tự
Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số
y
1
3
x
3
-
m
x
2
+
(
m
2
-
1
)
x
có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y 5x- 9 . Tính tổng tất cả các phần tử của S. A. 0. B. 6. C. -6. D. 3.
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - m x 2 + ( m 2 - 1 ) x có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y= 5x- 9 . Tính tổng tất cả các phần tử của S.
A. 0.
B. 6.
C. -6.
D. 3.
Cho hàm số
y
x
3
-
3
x
2
+
4
có đồ thị (C) , đường thẳng (d): ym(x+1) với m là tham số, đường thẳng
∆
:
y
2
x
-
7
. Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với
∆
và...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C) , đường thẳng (d): y=m(x+1) với m là tham số, đường thẳng ∆ : y = 2 x - 7 . Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với ∆ và d B ; ∆ + d C ; ∆ = 6 5 .
A. 0
B. 8
C. 5
D. 4
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
y
-
x
-
1
3
+
3
m
x
-
1
-
2
có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử t...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2 3
C. 1.
D. 5.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+y²+ (z+2)²4 và đường thẳng
d
:
x
2
-
y
y
t
z
m
-
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+y²+ (z+2)²=4 và đường thẳng d : x = 2 - y y = t z = m - 1 + t . Gọi T là tập tất cả các giá trị của m để d cắt (S) tại hai điểm phân biệt A, B sao cho các tiếp diện của (S) tại A và B tạo với nhau góc lớn nhất có thể. Tính tổng các phần tử của tập hợp T.
A. 3
B. -3
C. -5.
D. -4.
Cho hàm số
y
2
x
+
1
x
+
1
có đồ thị (C) . Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d: y x+m-1 cắt (C) tại hai điểm phân biệt A; B thỏa mãn
A
B
2
3
A.
m
2
±
10...
Đọc tiếp
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C) . Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d: y= x+m-1 cắt (C) tại hai điểm phân biệt A; B thỏa mãn A B = 2 3
A. m = 2 ± 10
B. m = 4 ± 10
C. m = 4 ± 3
D. m = 2 ± 3
Cho hàm số
y
f
x
có đồ thị như hình bên dưới Gọi S là tập hợp tất cả các giá trị nguyên của tham số
m
∈
-
100
;
100
để hàm số
h
x
f
2
x
+
2...
Đọc tiếp
Cho hàm số y = f x có đồ thị như hình bên dưới
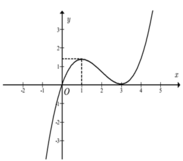
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m ∈ - 100 ; 100 để hàm số h x = f 2 x + 2 + 4 f x + 2 + 3 m có đúng 3 điểm cực trị. Tổng giá trị của tất cả các phần tử thuộc S bằng
Cho hàm số
y
x
3
-
3
x
2
+
m
, với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + m , với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là
Tập tất cả các giá trị của tham số m để đường thẳng
d
:
y
x
+
m
2
cắt đồ thị hàm số
(
C
)
:
y
-
x
3
+
4
x
tại ba điểm phân biệt là A. (-1;1) B.
(
-
∞...
Đọc tiếp
Tập tất cả các giá trị của tham số m để đường thẳng d : y = x + m 2 cắt đồ thị hàm số ( C ) : y = - x 3 + 4 x tại ba điểm phân biệt là
A. (-1;1)
B. ( - ∞ ; 1 ]
C. R
D. - 2 ; 2
Tập hợp tất cả các giá trị của tham số m để đường thẳng ymx+1 cắt đồ thị hàm số
y
x
−
3
x
+
1
tạo hai điểm phân biệt là A.
−
∞
;
0
∪
16
;
+
∞
B. ...
Đọc tiếp
Tập hợp tất cả các giá trị của tham số m để đường thẳng y=mx+1 cắt đồ thị hàm số y = x − 3 x + 1 tạo hai điểm phân biệt là
A. − ∞ ; 0 ∪ 16 ; + ∞
B. − ∞ ; 0 ∪ 16 ; + ∞
C. 16 ; + ∞
D. − ∞ ; 0