\(y'=4x^3-4x=0\Rightarrow\left\{{}\begin{matrix}x=0\Rightarrow y=2\\x=1\Rightarrow y=1\\x=-1\Rightarrow y=1\end{matrix}\right.\)

\(S=\dfrac{1}{2}.\left(2-1\right)\left(1-\left(-1\right)\right)=1\)

Đáp án D

Có f ' x = 8 x 3 − 8 x ;   f ' x = 0 ⇔ x = 0 x = 1 x = − 1  

Từ đó 3 điểm cực trị là A − 1 ; 1 ; B 0 ; 3 ; C 1 ; 1 .

Nhận thấy rằng A B C  là tam giác cân tại B với đường cao là BM , M là trung điểm của AC.

Tinh được A C = 2 ; B M = 2 ⇒ S A B C = 1 2 .2.2 = 2 .

Đáp án D

Đáp án D

Ta có:  y = f ' x = 4 x 3 − 4 x = 4 x x 2 − 1 ⇔ x = 0 x = ± 1

=> Các điểm cực trị là A 0 ; 3 , B 1 ; 2 , C − 1 ; 2 ⇒ Δ A B C  cân tại

A ; B C = 1 + 1 2 + 2 − 2 2 = 2

Gọi I là trung điểm của  B C ⇒ I 0 ; 2 ⇒ A I = h = 1

Ta có:  S = 1 2 A I . B C = 1

Cách 2: Áp dụng CT giải nhanh:  S = b 2 4 a . − b 2 a = 1

Đáp án D

Ta có

y ' = 4 x 3 − 4 x = 0 ⇔ x = 0 ⇒ y = 3 ⇒ A 0 ; 3 x = ± 1 ⇒ y = 2 ⇒ B 1 ; 2 , C − 1 ; 2

⇒ A B → = − 2 ; 0 ⇒ B C = 2 B C : y = 2 ⇒ d A ; B C = 1 ⇒ S A B C = 1 2 B C . d A ; B C = 1

Đáp án C

Ta có y ' = 4 x 3 − 4 x ; y ' = 0 ⇔ x = 0 ⇒ y 0 = 2 x = ± 1 ⇒ y ± 1 = 1  

Suy ra 3 điểm cực trị của ĐTHS là A 0 ; 2 ,   B 1 ; 1 ,   C − 1 ; 1  

Khi đó  A B = A C = 2 , B C = 2 ⇒ S Δ A B C = 1 2 A B 2 = 2 2 2 = 1

\(y'=4x^3-4mx=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=m\end{matrix}\right.\)

Hàm có 3 cực trị khi \(m>0\)

Gọi 3 cực trị là A; B; C với \(\left\{{}\begin{matrix}A\left(0;m^4+2m\right)\\B\left(\sqrt{m};2m\right)\\C\left(-\sqrt{m};2m\right)\end{matrix}\right.\)

Tam giác ABC luôn cân tại A, gọi H là trung điểm BC \(\Rightarrow H\left(0;2m\right)\)

\(AH=\left|y_A-y_H\right|=m^4\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{m}\)

\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.m^4.2\sqrt{m}=4\)

\(\Leftrightarrow m^9=16\Rightarrow m=\sqrt[3]{2}\)

Đáp án C

Ta có: y’ = 8x³ – 8x

ð y’ = 0 ó x = 0 hoặc x = 1 hoặc x = -1

Ta có bảng biến thiên:

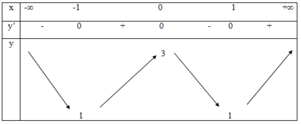
Vậy các điểm cực trị của hàm là: (-1;1), (0;3) và (1;1)

Theo công thức tính diện tích tam giác, ta có:

    S = p ( p − a ) ( p − b ) ( p − c )                                           

Trong đó

    p = a + b + c 2                                                     

Vậy diện tích tam giác tạo bởi 3 điểm cực trị của đồ thị hàm số là 2