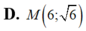Gọi M(x;y) là các điểm biểu diễn cho số phức z thỏa mãn log 1 3 z − 2 + 2 4 z − 2 − 1 > 1. Khi đó x ; y thỏa mãn hệ thức nào dưới đây?
A. x + 2 2 + y 2 > 49
B. x + 2 2 + y 2 < 49
C. x − 2 2 + y 2 < 49
D. x − 2 2 + y 2 > 49
Những câu hỏi liên quan
A gọi B bằng bác , B gọi C là ông nội ,C gọi D là cậu , D gọi E là gì ,E gọi F là chú , F gọi Z là con , Z gọi X là bố , X gọi V là cụ , V gọi M là chồng . hỏi A gọi M là gì .
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
cos
x
+
2
.
sin
x
+
3
2
.
cos
x...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos x + 2 . sin x + 3 2 . cos x - sin x + 4 . Tính M,m
A. 4/11
B. 3/4
C. 1/2
D. 20/11
Cho hai đa thức
P
(
x
)
−
6
x
5
−
4
x
4
+
3
x
2
−
2
x
;
Q
(
x
)
2
x
5
−
4
x
4
−
2
x
3...
Đọc tiếp
Cho hai đa thức P ( x ) = − 6 x 5 − 4 x 4 + 3 x 2 − 2 x ; Q ( x ) = 2 x 5 − 4 x 4 − 2 x 3 + 2 x 2 − x − 3
Gọi M(x) = P(x) - Q(x). Tính M(-1)
A. 11
B. -10
C. -11
D. 10
Ta có
M ( x ) = P ( x ) − Q ( x ) = − 6 x 5 − 4 x 4 + 3 x 2 − 2 x − 2 x 5 − 4 x 4 − 2 x 3 + 2 x 2 − x − 3 = − 8 x 5 + 2 x 3 + x 2 − x + 3 Có M ( − 1 ) = − 8. ( − 1 ) 5 + 2 ⋅ ( − 1 ) 3 + ( − 1 ) 2 − ( − 1 ) + 3 = 11
Chọn đáp án A
Đúng 0
Bình luận (0)
Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y
x
-
1
+
3
-
x
thì M+
2
m bằng A.
2
2
+
1
B. 4 C.
2
+
2
D. 3
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y= x - 1 + 3 - x thì M+ 2 m bằng
A. 2 2 + 1
B. 4
C. 2 + 2
D. 3
Gọi M, m lần lượt là GTLN, GTNN của hàm số y = x - 1 + 7 - x . Khi đó có bao nhiêu số nguyên nằm giữa m, M ?
A. 1
B. 2
C. Vô số
D. 0
Chọn A.
ĐK: 1 ≤ x ≤ 7
Ta có 
Xét y(1) = y(7) = 6 , y(4) = 2 3 suy ra 2,44 < k < 3,464 suy ra k = 3 có 1 số nguyên k.
Đúng 0
Bình luận (0)
Cho PT: \(x^2+\left(m+1\right)x+m-1=0\left(1\right)\)
Gọi x1, x2 là 2 nghiệm của PT (1). Tìm m để \(x^2_1x_2+x^2_2x_1=-8\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-m-1\\x_1.x_2=m-1\end{matrix}\right.\)
\(x_1^2x_2+x_2^2x_1=-8\)
\(\Leftrightarrow x_1x_2\left(x_1+x_2\right)=-8\)
\(\Leftrightarrow\left(m-1\right)\left(-m-1\right)=-8\)
\(\Leftrightarrow-m^2-m+m+1=-8\)
\(\Leftrightarrow-m^2+9=0\)
\(\Leftrightarrow-m^2=-9\)
\(\Leftrightarrow m=\pm\sqrt{3}\)
Đúng 0
Bình luận (0)
Do pt có 2 nghiệm \(x_1,x_2\) nên theo đ/l Vi-ét , ta có :
\(\left\{{}\begin{matrix}S=x_1+x_2=-\dfrac{b}{a}=-m-1\\P=x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
Ta có :
\(x_1^2x_2+x_2^2x_1=-8\)
\(\Leftrightarrow x_1x_2\left(x_1+x_2\right)=-8\)
\(\Leftrightarrow P.S+8=0\)
\(\Leftrightarrow\left(m-1\right).\left(-m-1\right)+8=0\)
\(\Leftrightarrow-m^2-m+m+1+8=0\)
\(\Leftrightarrow-m^2+9=0\)
\(\Leftrightarrow-m^2=-9\)
\(\Leftrightarrow m^2=9\)
\(\Leftrightarrow m=\pm3\)
Đúng 2
Bình luận (0)
1. Gọi x là tổng các.chức số a = 3^2010+2011 gọi y là tổng các chữ số của x, gọi z là tổng các chữ số của y. Tìm z
2. Tìm x £ N
a) 41— 2^x—1=9
b) |x—3|—21= _5
d) 6M+7= 7^x+1 với M = 7+7^2+7^3+...+7^2016
g) x+9 chia hết x—2
3. Tìm x, y biết:
a) ( x + 1)^100+|y—3| =0
Bài 2:
\(41-2^x-1=9\)
\(\Rightarrow40-2^x=9\)
\(\Rightarrow2^x=31\)
\(\Rightarrow x\in\left\{\varnothing\right\}\)
Vậy không có giá trị x thỏa mãn
b) \(\left|x-3\right|-21=-5\)
\(\Rightarrow\left|x-3\right|=16\)
\(\Rightarrow x-3=\pm16\)
+) \(x-3=16\Rightarrow x=19\)
+) \(x-3=-16\Rightarrow x=-13\)
Vậy \(x\in\left\{19;-13\right\}\)
d) Ta có: \(M=7+7^2+...+7^{2016}\)
\(\Rightarrow7M=7^2+7^3+...+7^{2017}\)
\(\Rightarrow7M-M=\left(7^2+7^3+...+7^{2017}\right)-\left(7+7^2+...+7^{2016}\right)\)
\(\Rightarrow6M=7^{2017}-7\)
\(6M+7=7^{x+1}\)
\(\Rightarrow7^{2017}-7+7=7^{x-1}\)
\(\Rightarrow7^{x-1}=7^{2017}\)
\(\Rightarrow x-1=2017\)
\(\Rightarrow x=2018\)
Vậy \(x=2018\)
g) Ta có: \(x+9⋮x-2\)
\(\Rightarrow\left(x-2\right)+11⋮x-2\)
\(\Rightarrow11⋮x-2\)
\(\Rightarrow x-2\in\left\{1;-1;11;-11\right\}\)
+) \(x-2=1\Rightarrow x=3\)
+) \(x-2=-1\Rightarrow x=1\)
+) \(x-2=11\Rightarrow x=13\)
+) \(x-2=-11\Rightarrow x=-9\)
Vậy \(x\in\left\{3;1;13;-9\right\}\)
Bài 3:
a) \(\left(x+1\right)^{100}+\left|y-3\right|=0\)
\(\Rightarrow\left(x+1\right)^{100}=0\) và \(\left|y-3\right|=0\)
+) \(\left(x+1\right)^{100}=0\Rightarrow x+1=0\Rightarrow x=-1\)
+) \(\left|y-3\right|=0\Rightarrow y-3=0\Rightarrow y=3\)
Vậy \(x=-1;y=3\)
Đúng 0
Bình luận (1)
Cho mặt phẳng
P
:
x
+
m
z
-
m
0
và mặt phẳng
Q
:
(
1
-
m
)
x
-
m
y
0
(tham số
m
#
0
). Gọi
d
P
∩
Q
. Xét các mặt phẳng...
Đọc tiếp
Cho mặt phẳng P : x + m z - m = 0 và mặt phẳng Q : ( 1 - m ) x - m y = 0 (tham số m # 0 ). Gọi d = P ∩ Q . Xét các mặt phẳng α chứa (d), xét điểm A 2 ; 1 ; 1 . Khi đó gọi h là khoảng cách từ A đến (d) thì GTLN của h h m a x bằng bao nhiêu?
Cho pt \(x^2-(2m+3)x+m=0\). Gọi \(x_1,x_2\) là các nghiệm của pt. Tìm giá trị của m để \(x^2_1+x^2_2\) đạt GTNN
\(\Delta=\left(2m+3\right)^2-4m=4m^2+12m+9-4m=4m^2+8m+9\)
\(=4\left(m^2+2m+1-1\right)+9=4\left(m+1\right)^2+5\ge5>0\forall m\)
Vậy pt luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=2m+3\\x_1x_2=m\end{matrix}\right.\)Ta có : \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(\left(2m+3\right)^2-2m=4m^2+12m+9-2m=4m^2+10m+9\)
\(=4m^2+\dfrac{2.2m.10}{4}+\dfrac{100}{16}-\dfrac{100}{16}+9\)
\(=\left(2m+\dfrac{10}{4}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall m\)
Dấu ''='' xảy ra khi x = -5/4
Đúng 1
Bình luận (0)
Cho đồ thị
(
C
)
:
y
x
Gọi M là điểm thuộc (C), A(9;0). Gọi S1 là diện tích hình phẳng giứi hạn bởi (C), đường thẳng x 9 và trục hoành; S2 là diện tích tam giác OMA. Tọa độ điểm M để S1 2S2 là:
Đọc tiếp
Cho đồ thị ( C ) : y = x Gọi M là điểm thuộc (C), A(9;0). Gọi S1 là diện tích hình phẳng giứi hạn bởi (C), đường thẳng x = 9 và trục hoành; S2 là diện tích tam giác OMA. Tọa độ điểm M để S1 = 2S2 là:
