tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số trên đoạn [2;4]
y=\(\dfrac{x^2+3}{x-1}\)
Cho hàm số y =
-
x
2
+
2
n
ế
u
-
2
≤
x
≤
1
x
n
ế
u
1
<
x
≤
3
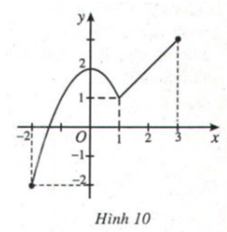
Có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] và nêu cách tính.
Giá trị nhỏ nhất của hàm số trên đoạn [-2,3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại x = -2. Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.
Giá trị lớn nhất của hàm số trên đoạn [-2,3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại x = 3. Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f(x) = x 2 − 4x + 3 trên đoạn [−2; 1].
A. M = 15; m = 1.
B. M = 15; m = 0.
C. M = 1; m = −2.
D. M = 0; m = −15.
Tính giá trị lớn nhất và nhỏ nhất của hàm số:
y = 2 - x 1 - x trên các đoạn [2 ; 4] và [-3 ; -2]
TXĐ: D = (-∞; 1) ∪ (1; +∞)
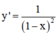> 0 với ∀ x ∈ D.
⇒ hàm số đồng biến trên (-∞; 1) và (1; +∞).
⇒ Hàm số đồng biến trên [2; 4] và [-3; -2]
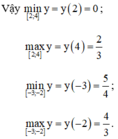
Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
\(y=x^3-3x^2-9x+35\) trên các đoạn [-4; 4] và [0;5] ;
\(y'=3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
a. Trên [-4;4] ta có:
\(y\left(-4\right)=-41\) ; \(y\left(-1\right)=40\) ; \(y\left(3\right)=8\) ; \(y\left(4\right)=15\)
\(\Rightarrow y_{min}=-41\) ; \(y_{max}=40\)
b. Trên [0;5] ta có:
\(y\left(0\right)=35\) ; \(y\left(3\right)=8\); \(y\left(5\right)=40\)
\(\Rightarrow y_{max}=40\) ; \(y_{min}=8\)
Tìm giá trị lớn nhất của hàm số \(y=x^2-2x+3\) trên đoạn \(\left[0;4\right]\)
\(y=f\left(x\right)=x^2-2x+3\)
\(f\left(0\right)=3;f\left(4\right)=11;f\left(1\right)=2\)
\(\Rightarrow max=f\left(4\right)=11\Leftrightarrow x=4\)
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.
A. 2
B. 5
C. 4
D. 6
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau
Biết rằng f(0)+f(3)=f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là
A. f(0), f(5)
B. f(2), f(0)
C. f(1), f(5)
D. f(2), f(5)
Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
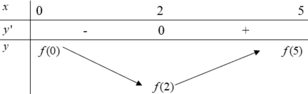
Suy ra 
Và 
Ta có 
Vì f(x) đồng biến trên đoạn [2;5] nên 
⇒ f(5)>f(0)
Vậy
Chọn đáp án D.
Giá trị lớn nhất của hàm số y=x-1/x+2 trên đoạn [0;1] là:
\(y'=\dfrac{3}{\left(x+2\right)^2}>0\Rightarrow\) hàm đồng biến trên đoạn đã cho
\(\Rightarrow\max\limits_{\left[0;1\right]}y=y\left(1\right)=0\)
Tìm giá trị lớn nhất của hàm số y=e^x(x^2-x-5) trên đoạn [1;3].
A.
B. 
C. 
D. 
