a) Vẽ đồ thị hàm số y = -x+3
b)Tính khoảng cách từ gốc tọa độ đến đồ thị hàm số
Bài 2: : Cho hàm số y= -2x +8
a. Vẽ đồ thị hàm số
b. Tính góc tạo bởi đồ thị hàm số với trục ox?
c. Tính khoảng cách từ gốc tọa độ đến đồ thị hàm số?
d. Điểm A(-1; 10 ) có thuộc đồ thị hàm số không?
e. Tính diện tích và chu vi của hình tạo bởi đồ thị hàm số với hai
trục tọa độ?
Giúp nhanh trong tối nay với ạ ;-;
Cho hàm số bậc nhất y = (m + 1) . x - 2 có đồ thị là đường thẳng (d). Trong đó m là tham số, m \(\neq\) -1.
a) Vẽ đồ thị hàm số và tính khoảng cách từ gốc tọa độ đến đồ thị hàm số với m = 1 (đơn vị đo trên các trục tọa độ là cm).
b) Tìm giá trị của m để đồ thị hàm số đã cho cắt đồ thị hàm số y = x - 1 tại một điểm có hoành độ là 3.
Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A. -4
B. -5
C. -6.
D. -7
Ta có y’ = 3x2- 6mx + 3( m2-1).
Hàm số đã cho có cực trị thì phương trình y’ =0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nghiệm phân biệt ⇔ ∆ = 1 > 0 , ∀ m
Khi đó, điểm cực đại A( m-1; 2-2m) và điểm cực tiểu B( m+1; -2-2m)
Ta có
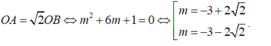
Tổng hai giá trị này là -6.
Chọn C.
cho hàm số y=2x-4
a)vẽ đồ thị (d) của hàm số y=2x-4
b) tính khoảng cách từ gốc tọa độ O đến đường thẳng (d) đơn vị trên trục tọa độ là cm
c)Xác định các hệ số a và b của hàm số y=ax+b, biết rằng đồ thị (d') của hàm số này song song với (d) đi qua điểm A (0;3)
\(b,\) PT giao Ox và Oy:
\(y=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\\ x=0\Leftrightarrow y=-4\Leftrightarrow B\left(0;-4\right)\Leftrightarrow OB=4\)
Gọi H là chân đường cao từ O đến (d)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{4}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Leftrightarrow OH^2=\dfrac{16}{5}\Leftrightarrow OH=\dfrac{4}{\sqrt{5}}\left(cm\right)\)
Vậy k/c là \(\dfrac{4}{\sqrt{5}}\left(cm\right)\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne-4\\0a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
Bài 4. Cho các hàm số: y =3x và y =-3x +4
1)Vẽ trên cùng hệ trục tọa độ, đồ thị hai hàm số đã cho.
2)Tìm tọa độ giao điểm M của đồ thị hai hàm số trên bằng phép toán.
3)Tính khoảng cách từ O ( gốc tọa độ) đến đường thẳng y =-3x +4.
4)Trong các điểm: C(\(\dfrac{1}{3};3\)) ; D(2;10) điểm nào thuộc, điểm nào không thuộc đồ thịhàm số y= -3x+4. Vì sao?
5)Tìm trên đường thẳng y =-3x+4 điểm có hoành độ bằng x=\(\dfrac{2}{3}\) .
6) Tìm trên đường thẳng y =-3x+4 điểm có tung độ bằng y = -2 .
7) Tìm trên đường thẳng y =-3x +4 điểm M (x;y) sao cho y2+ xy -2x2=0.
8) Tìm trên đường thẳng y =-3x+4 điểm N(x;y) sao cho khoảng cách từ N đến Ox bằng 4 lần khoảng cách từ N đến Oy
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
![]()
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
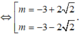
Cho hàm số y= 2x-3 có đồ thị (D)
a) Vẽ đồ thị (D)
b)Tính khoảng cách từ gốc tọa độ đến (D)
c) Tính góc a tạo bởi đường thẳng (D) và trục Ox.(Làm tròn đến phút)
Cho hai hàm số sau y = – x + 4 và y = 3x a/ Vẽ trên cùng một mặt phẳng tọa độ đồ thị hai hàm số trên. b/ Tìm tọa độ giao điểm của hai hàm số đó. c/ Tính khoảng cách từ gốc tọa độ đến đường thẳng y = – x + 4 (kết quả làm tròn đến chữ số thập phân thứ 3) ( chỉ mình câu c thôi nha câu c mình k bt làm :( )
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x=-x+4\\y=3x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
c: Gọi A,B lần lượt là giao điểm của đường thẳng y=-x+4 đến hai trục Ox, Oy
Tọa độ điểm A là: \(\left\{{}\begin{matrix}y_A=0\\4-x=0\end{matrix}\right.\Leftrightarrow A\left(4;0\right)\)
Tọa độ điểm B là: \(\left\{{}\begin{matrix}x_A=0\\y=-0+4=4\end{matrix}\right.\Leftrightarrow B\left(0;4\right)\)
\(AB=\sqrt{\left(0-4\right)^2+\left(4-0\right)^2}=4\sqrt{2}\)
Khoảng cách từ O đến đường thẳng y=-x+4 là:
\(AH=\dfrac{OA\cdot OB}{AB}=\dfrac{16}{4\sqrt{2}}=2\sqrt{2}\)
Tọa độ giao điểm là:
{3x=−x+4y=3x⇔{x=1y=3{3x=−x+4y=3x⇔{x=1y=3
c: Gọi A,B lần lượt là giao điểm của đường thẳng y=-x+4 đến hai trục Ox, Oy
Tọa độ điểm A là: {yA=04−x=0⇔A(4;0){yA=04−x=0⇔A(4;0)
Tọa độ điểm B là: {xA=0y=−0+4=4⇔B(0;4){xA=0y=−0+4=4⇔B(0;4)
AB=√(0−4)2+(4−0)2=4√2AB=(0−4)2+(4−0)2=42
Khoảng cách từ O đến đường thẳng y=-x+4 là:
Cho hàm số y=3x
a) Vẽ đồ thị hàm số
b) Điểm A thuộc đồ thị hàm số có khoảng cách tới gốc tọa độ là \(2\sqrt{10}\). Xác định tọa độ của A.
Lời giải:
a. Hình vẽ:
b. Vì điểm $A$ thuộc đths nên $A$ có tọa độ $(a,3a)$
$OA=\sqrt{a^2+(3a)^2}=2\sqrt{10}$
$\sqrt{10a^2}=2\sqrt{10}$
$10a^2=400$
$a=\pm 2$
Vậy tọa độ điểm A là $(2,6)$ hoặc $(-2,-6)$