Khai triển biểu thức ( 1 - 2 x ) n ta được đa thức có dạng a 0 + a 1 x + a 2 x 2 + . . . + a n x n . Tìm hệ số của x 5 biết a 0 + a 1 + a 2 = 71
A. -648
B. -876
C. -672
D. -568
Những câu hỏi liên quan
Khai triển biểu thức
1
-
2
x
n
ta được đa thức có dạng
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
n
x
n...
Đọc tiếp
Khai triển biểu thức 1 - 2 x n ta được đa thức có dạng a 0 + a 1 x + a 2 x 2 + . . . + a n x n . Tìm hệ số của x 5 biết a 0 + a 1 + a 2 = 71
A. -648
B. -876
C. -672
D. -568
11 tháng 4 2021 lúc 15:47
Tìm hệ số của \(x^4\) trong khai triển của biểu thức P = \(\left(1-x-3x^3\right)^n\) thành đa thức, biết n là số nguyên dương thoả mãn \(2\left(C^2_2+C^2_3+...+C^2_n\right)=3A^2_{n+1}\).
\(C_2^2+C_3^2+...+C_n^2=C_3^3+C_3^2+C_4^2+...+C_n^2\) (do \(C_2^2=C_3^3=1\))
\(=C_4^3+C_4^2+C_5^2+...+C_n^2=C_5^3+C_5^2+...+C_n^2\)
\(=...=C_n^3+C_n^2=C_{n+1}^3\)
Do đó:
\(2C_{n+1}^3=3A_{n+1}^2\Leftrightarrow\dfrac{2.\left(n+1\right)!}{3!.\left(n-2\right)!}=\dfrac{3.\left(n+1\right)!}{\left(n-1\right)!}\)
\(\Leftrightarrow n-1=9\Rightarrow n=10\)
\(\Rightarrow P=\left(1-x-3x^3\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(-x-3x^3\right)^k\)
\(=\sum\limits^{10}_{k=0}C_{10}^k\left(-1\right)^k\left(x+3x^3\right)^k=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^kx^i.3^{k-i}.x^{3\left(k-i\right)}\)
\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^k.3^{k-i}.x^{3k-2i}\)
Ta có: \(\left\{{}\begin{matrix}0\le i\le k\le10\\i;k\in N\\3k-2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(1;2\right);\left(4;4\right)\)
Hệ số: \(C_{10}^2C_2^1\left(-1\right)^2.3^1+C_{10}^4C_4^4.\left(-1\right)^4.3^0=...\)
Đúng 1
Bình luận (1)
\(\Rightarrow he-so:\left[{}\begin{matrix}C^9_{10}C^1_9\left(-3\right)^{10-9}\left(-1\right)=270\\C^{10}_{10}C^4_{10}\left(-3\right)^{10-10}.\left(-1\right)^4=210\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho đa thức q(x) = (3x3 - 2x2 + 3x - 4)10 khi khai triển đa thức q(x) ta được đa thức f(x) . Sắp xếp theo thứ tự giảm dần của biến. Tính tổng các hệ số f(x).
Chào bạn. Mời bạn tham khảo ứng dụng tự động cân bằng phương trình và từ điển phương trình hóa học trên điện thoại. Android: https://goo.gl/jv8qfC . IOS(Iphone): https://goo.gl/BQ2Kqo . Clip hướng dẫn: https://youtu.be/qDpsKPwPAto . Bạn copy link vào trình duyệt nhé!
Đúng 0
Bình luận (0)
Tổng các hệ số của f(x) cũng là tổng các hệ số của q(x)
Tổng hệ số của q(x) là giá trị của q(x) tại x=1
\(q\left(1\right)=\left(3.1^3-2.1^2+3.1-4\right)^{10}=0\)
Đúng 0
Bình luận (0)
khai triển đa thức : (27x3 - 1) ta được :
@Jena
(27 x 3 - 1)
= (27 x 3) - 1
= 81 - 1
= 80
Đúng 0
Bình luận (1)
Cho Khai triển P(x) thành đa thức ta được Tính A.
S
-
20
.
5
19
B.
S
20
.
5
21
C.
S...
Đọc tiếp
Cho 
Khai triển P(x) thành đa thức ta được 
Tính 
A. S = - 20 . 5 19
B. S = 20 . 5 21
C. S = 20 . 5 19
D. S = 20 . 5 20
Đáp án D
Phương pháp:
Công thức nhị thức Newton 
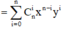
Cách giải:
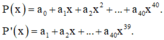
Ta có 
Cho x =1
Đúng 0
Bình luận (0)
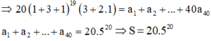
Câu 2. (2 điểm) Cho biểu thức $Q=(x y-1)^5$.
a) Viết khai triển biểu thức $Q$ bằng nhị thức Newton.
b) Tìm số hạng có chứa $x^2 y^2$ trong khai triển trên.
Cho đa thức:
P
(
x
)
(
1
+
x
)
8
+
(
1
+
x
)
9
+
(
1
+
x
)
10
+
(
1
+...
Đọc tiếp
Cho đa thức: P ( x ) = ( 1 + x ) 8 + ( 1 + x ) 9 + ( 1 + x ) 10 + ( 1 + x ) 11 + ( 1 + x ) 12 . Khai triển và rú gọn ta được đa thức: P ( x ) = a o + a 1 x + a 2 x 2 + . . . + a 12 x 12 . Tìm hệ số a 8
A. 700
B. 715
C. 720
D. 730
Chọn B
Ta có a8= C88+C98+C108+C118+C128= 1+9+45+165+495= 715
Đúng 0
Bình luận (0)
Khai triển và rút gọn biểu thức
1
-
x
+
2
1
-
x
2
+
.
.
.
+
n
1
-
x
n
thu được đa thức
P
x...
Đọc tiếp
Khai triển và rút gọn biểu thức 1 - x + 2 1 - x 2 + . . . + n 1 - x n thu được đa thức P x = a 0 + a 1 x + . . . + a n x n . Tính hệ số a 8 biết rằng n là số nguyên dương thỏa mãn 1 C n 2 + 7 C n 3 = 1 n
A. 79
B. 99
C. 89
D. 97
Khai triển và rút gọn biểu thức
1
-
x
+
2
1
-
x
2
+
.
+
n
1
-
x
n
thu được đa thức
P
x
a
0
+
a
1...
Đọc tiếp
Khai triển và rút gọn biểu thức
1 - x + 2 1 - x 2 + . + n 1 - x n thu được đa thức
P x = a 0 + a 1 x + . . + a n x n . Tính hệ số a 8 biết rằng n là số nguyên dương thỏa mãn 1 C n 2 + 7 C n 3 = 1 n
A. 79
B. 99
C. 89
D. 97
Ta có
1 C n 2 + 7 C n 3 = 1 n ⇔ n ≥ 3 2 n n - 1 + 7 . 3 ! n n - 1 n - 2 = 1 n ⇔ n ≥ 3 n 2 - 5 n - 36 = 0 ⇔ n = 9
Suy ra a 8 là hệ số của x 8 trong khai triển 8 1 - x 8 + 9 1 - x 9
Vậy ta thu được a 8 = 8 . C 8 8 + 9 . C 9 8 = 89
Đáp án C
Đúng 0
Bình luận (0)