Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
Pham Trong Bach
Tìm tất cả các giá trị của m để phương trình m x 2017 x 2018 − 1 + x − 2 0  có nghiệm. A.  m ∈ ℝ B.  m ∈ ℝ { 0 } C.  m ∈ − 1...
Đọc tiếp
Lớp 0 Toán
Những câu hỏi liên quan
Sofia Nàng

Cho phương trình x² - (2m + 2)x + 2m = 0 (1), với m là tham số. Tìm tất cả các giá trị của m để phương trình (1) nhận 4 + √2017 là một nghiệm.

Xem chi tiết
Lớp 9 Toán Câu hỏi của OLM

Khách
 
Đỗ Nguyễn Phương Thùy
27 tháng 5 2020 lúc 22:38

THAY X=4+\(\sqrt{2017}\)VÀO PHƯƠNG TRÌNH=>PT CÓ DẠNG ;GÌ ĐÓ GÌ ĐÓ VIẾT RA NHEN<lười chảy nước>

cho pt cộng với chất xúc tác cho ló pư nhanh(hehe)....=\(2025+6\sqrt{2017}-6m-2m\sqrt{2017}=0\)

=>\(0m^2-\left(6+2\sqrt{2017}\right)m+2025+6\sqrt{2017}=0\)rùi tự giải đenta nha, mệt mỏi qué rùi tui coằn ik ngủ mai kiểm tra, nếu rảnh mai tui qua cho kết quả nha sỏ ry nhìu

Bình luận (0)
 Khách vãng lai đã xóa
Đỗ Nguyễn Phương Thùy
28 tháng 5 2020 lúc 20:55

chắc qua bùn ngủ qué ko giải đenta nha^,^

m=\(\frac{2025+6\sqrt{2017}}{6+2\sqrt{2017}}\)

Bình luận (0)
 Khách vãng lai đã xóa
Pham Trong Bach
Tìm tất cả các giá trị thực của tham số m để phương trình 5 x 2 + 12 x + 16 m ( x + 2 ) x 2 + 2...
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
11 tháng 5 2018 lúc 17:42

Đáp án đúng : A

Bình luận (0)
Pham Trong Bach
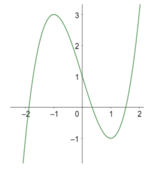
Cho hàm số y f(x) xác định trên ℝ và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m - 2018 0 có duy nhất một nghiệm. A. m ≤ 2015, m  ≥ 2019. B. 2015 m 2019. C. m 2015, m 2019. D. m  2015, m  2019.
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
31 tháng 5 2018 lúc 16:06

Chọn D

Phương pháp:

Biến đổi phương trình về f(x) = 2018 - m và sử dụng tương giao đồ thị: Phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng y = 2018 - m cắt đồ thị hàm số y = f(x) tại duy nhất một điểm.

Cách giải:

Phương trình f(x) + m - 2018 = 0 

 

Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2018 - m (có phương song song hoặc trùng với trục hoành).

Dựa vào đồ thị, ta có ycbt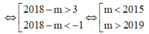 

Bình luận (0)
Pham Trong Bach
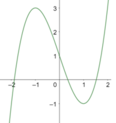
Cho hàm số yf(x) xác định trên R và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x)+m-20180 có duy nhất một nghiệm. A. m ≤ 2015 , m ≥ 2019 . B.2015m2019 C.m2015,m2019 D.m2015,m2019
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
18 tháng 11 2018 lúc 17:31

Bình luận (0)
Thạch Tít

Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x - 2018) - 2| = m có đúng 3 nghiệm

Xem chi tiết
Lớp 10 Toán Câu hỏi của OLM

Khách
 
Pham Trong Bach

Cho phương trình log 2  x = m  với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực.

A.  m ≥ 0

B.  m ∈ ℝ

C. m > 0

D.  m ∈ ℤ

Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
24 tháng 11 2019 lúc 2:48

Đáp án là B

Tập giá trị của hàm số  log a x = R

Bình luận (0)
Phùng Minh Phúc

Cho phương trình \(x^2-2\left(m+1\right)x+m^2-1=0\). Tìm tất cả các giá trị của m để phương trình có nghiệm

Xem chi tiết
Lớp 9 Toán

Khách
 
missing you =
8 tháng 5 2021 lúc 19:40

phương trình có nghiệm khi:

\(\Delta\)\(\ge\)0<=>[-(2m+1)]^2-4.(m^2-1)\(\ge\)0

<=>(2m+2)^2-4m^2+4\(\ge\)0

<=>4m^2+8m+4-4m^2+4\(\ge\)0

<=>8m+8\(\ge\)0

<=>8(m+1)\(\ge\)0

<=>m\(\ge\)-1

vậy m\(\ge\)-1 thì phương trình có nghiệm

Bình luận (0)
Trần văn dương
8 tháng 5 2021 lúc 21:33

△≥0⇔(2m+2)^2-4(m^2-1)≥0

⇔4m^2+8m+4-4m^2+4≥0

⇔8m+8≥0

⇔m≥-1

Vậy phương trình có nghiệm khi m≥-1

Bình luận (0)
Pham Trong Bach

Tìm tất cả các giá trị của tham số m để bất phương trình m( x - 1 ) < 3 - x có nghiệm?

A. m ≠ 1   

B. m = 1 

C. m ∈ R   

D. m ≠ 3 

Xem chi tiết
Lớp 8 Toán

Khách
 
Cao Minh Tâm
16 tháng 7 2019 lúc 4:44

Ta có: m(x - 1) < 3 – x

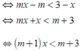
Bài tập tổng hợp chương 4 Đại số 8 | Lý thuyết và Bài tập Toán 8 có đáp án

Bất phương trình tương đương là ( m + 1 )x < m + 3

Rõ ràng với m ≠ - 1 thì bất phương trình luôn có nghiệm

Với m = - 1 ta có bất phương trình có dạng: 0x < 2 luôn đúng với mọi x

Vậy bất phương trình có nghiệm với mọi m.

Chọn đáp án C.

Bình luận (0)
Cao Tường Vi

3: cho hàm số f(x)=ax^2+bx+c có tọa độ đỉnh (2;-1) và có giá trị nhỏ nhất khi là -1 khi x=2
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x-2018)-2|=m có đúng 3 nghiệm.

Xem chi tiết
Lớp 10 Toán Câu hỏi của OLM

Khách
 
Trần Công Thanh Tài

Tìm tất cả các giá trị của tham số m để bất phương trình (m-1)x^2-(m-1)x+5 ≥ 0, ∀x ∈ R

Xem chi tiết
Lớp 10 Toán

Khách
 
Nguyễn Lê Phước Thịnh
16 tháng 3 2022 lúc 20:44

Để bất phương trình luôn có nghiệm thì 

\(\left\{{}\begin{matrix}\left(m-1\right)^2-4\cdot1\cdot5< 0\\1>=0\end{matrix}\right.\Leftrightarrow\left(m-1\right)^2< 20\)

\(\Leftrightarrow-2\sqrt{5}+1< x< 2\sqrt{5}+1\)

Bình luận (0)