điểm đối xứng với điểm M(-4;-4) qua trục Oy là điểm A'(__;__)

Những câu hỏi liên quan
cho điểm A(2;6), B(-3;-4), C(4;0)
a) tìm điểm A1 đối xứng với A qua Ox
b) tìm điểm A2 đối xứng với A qua Oy
c) tìm điểm A3 đối xứng với A qua B
d) tìm điểm A4 đối xứng với A qua BC
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).
a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.
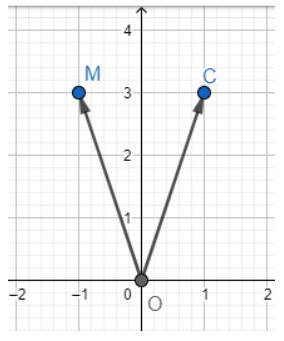
c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
a) Dựa vào hình vẽ ta thấy \(A\left( {1; - 3} \right)\)
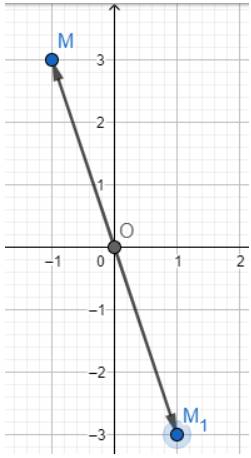
b) Dựa vào hình vẽ ta thấy \(B\left( { - 1; - 3} \right)\)

c) Dựa vào hình vẽ ta thấy \(C\left( {1;3} \right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, trung tuyến AM. Gọi I là trung điểm của AB; N là điểm đối xứng với M qua I, E là điểm đối xứng với M qua AC, D là điểm đối xứng với A qua M.
Chứng minh điểm E đối xứng với điểm N qua A.
Tam giác ABC cần thêm điều kiện gì thì tứ giác AECB là hình thang cân.
Bài 4: (3,5 điểm) Cho tam giác ABC vuông tại A. AH vuông góc với BC (H thuộc BC). Điểm E đối xứng với H qua AB, điểm F đối xứng với H qua AC. AB cắt EH tại M. AC cắt HF tại N.
a) Tứ giác AMHN là hình gì? Vì sao?
b) C/m E đối xứng với F qua A
c) Kẻ trung tuyến AI của tam giác ABC .C/m AI vuông góc với MN
a: Ta có: E và H đối xứng nhau qua AB
nên AB là đường trung trực của EH
Suy ra: AB\(\perp\)EH tại M và M là trung điểm của EH
Ta có: H và F đối xứng nhau qua AC
nên AC là đường trung trực của HF
Suy ra: AC\(\perp\)HF tại N và N là trung điểm của FH
Xét tứ giác AMHN có
\(\widehat{MAN}=\widehat{ANH}=\widehat{AMH}=90^0\)
Do đó: AMHN là hình chữ nhật
Đúng 3
Bình luận (0)
Cho tam giác ABC, gọi M1 là một điểm tuỳ ý, M2 đối xứng với M1 qua A, M3 đối xứng với M2 qua B, M4 đối xứng với M3 qua C. Chứng minh: Trung điểm của M1M4 là một điểm cố định
Gọi S là trung điểm của M1M4. Ta đi c/m S là điểm cố định.
Trong \(\Delta\)M1M2M4 có: A là trung điểm M1M2; S là trung điểm M1M4 => AS là đường trung bình \(\Delta\)M1M2M4
=> AS = M2M4 /2 và AS // M2M4 (1)
Trong \(\Delta\)M2M3M4 có: B là trung điểm M2M3 ; C là trung điểm M3M4 => BC là đường trung bình \(\Delta\)M2M3M4
=> BC = M2M4 /2 và BC // M2M4 (2)
Từ (1) và (2) suy ra: AS = BC và AS // BC => Tứ giác ABCS là hình bình hành.
Ta thấy: Hình bình hành ABCS có 3 đỉnh A;B;C cố định nên đỉnh S cố định
=> Trung điểm của M1M4 là một điểm cố định (đpcm).
Đúng 0
Bình luận (0)
Bài đối xứng trục
1, Nêu cách vẽ điểm M' đối xứng với điểm M qua đường thẳng a
2,Nêu cách chứng minh M' đối xứng với M qua đường thẳng a
3,Thế nào là 2 hình đối xứng qua 1 đường thẳng
4,Thế nào là hình có trục đối xứng (cho ví dụ)
1. Vẽ điểm M' trên nửa mp có bờ là đường thẳng a không chứa điểm M sao cho đường thẳng a là đường trung trực của đoạn thẳng MM'.
~ Nhớ t.i.c.k ~
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có O là giao điểm hai đường chéo AC và BD. Gọi I là trung điểm BC, E đối xứng với O qua I.1.Chứng minh rằng: OE DA2.Chứng minh rằng: E đối xứng với A qua trung điểm J của đoạn OB3.Chứng minh rằng: SABCD 2SBOCE.4.M đối xứng với I qua J. Chứng minh rằng: ba điểm A, M, B thẳng hàng.5.Gọi K là giao điểm AI và BO. Chứng minh rằng: Ba điểm M, K, C thẳng hàng
Đọc tiếp
Cho hình thoi ABCD có O là giao điểm hai đường chéo AC và BD. Gọi I là trung điểm BC, E đối xứng với O qua I.
1.Chứng minh rằng: OE = DA
2.Chứng minh rằng: E đối xứng với A qua trung điểm J của đoạn OB
3.Chứng minh rằng: SABCD = 2SBOCE.
4.M đối xứng với I qua J. Chứng minh rằng: ba điểm A, M, B thẳng hàng.
5.Gọi K là giao điểm AI và BO. Chứng minh rằng: Ba điểm M, K, C thẳng hàng
1: OI=CD/2
=>OE=CD
hay OE=AD
Đúng 0
Bình luận (0)
Cho góc vuông xOy, điểm M nằm trong góc đó. Gọi N là điểm đối xứng với M qua Ox, P là điểm đối xứng với M qua Oy. Chứng minh rằng P và N đối xứng nhau qua O.
Gọi giao điểm của MN và Ox là điểm A; giao điểm của MN và Oy là điểm B.
Ta có: N là điểm đối xứng với M qua Ox (gt).
O \(\in\) Ox.
=> \(\left\{{}\begin{matrix}OA\perp MN.\\\text{ON = OM.(1)}\end{matrix}\right.\)
Ta có: P là điểm đối xứng với M qua Oy (gt).
O \(\in\) Oy.
=> \(\left\{{}\begin{matrix}OB\perp MP.\\\text{OM = OP.(2)}\end{matrix}\right.\)
Từ (1) và (2) => OP = ON = OM.
Xét tam giác NOM có: ON = OM (cmt).
=> Tam giác NOM cân tại O.
Mà OA là đường cao (do OA vuông góc MN).
=> OA là phân giác của ^NOM (Tính chất các đường trong tam giác cân).
=> ^NOA = ^AOM.
Xét tam giác MOP có: OP = OM (cmt).
=> Tam giác MOM cân tại O.
Mà OB là đường cao (do OB vuông góc MP).
=> OB là phân giác của ^MOP (Tính chất các đường trong tam giác cân).
=> ^MOB = ^BOP.
Ta có: ^NOA + ^AOM + ^MOB + ^BOP.
= 2. ^AOM + 2. ^MOB.
= 2. (^AOM + ^MOB).
= 2. ^AOB.
= 2. 90o = 180o.
=> 3 điểm N; O; P thẳng hàng.
Mà OP = ON (cmt).
=> O là trung điểm của NP.
=> P và N đối xứng nhau qua O (đpcm).
Đúng 2
Bình luận (0)
Cho tam giác ABC có E , D và f lần lượt là trung điểm của BC , Ca và AB . gọi M là tâm điểm đối xứng với D qua điểm E , N là điểm đối xứng với D qua điểm F . Chứng minh rằng điểm M đối xứng với điểm N qua điểm B


















