Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm 2 m ( c o s x + s i n x ) = 2 m 2 + c o s x - sin x + 3 2
A. - 1 2 > m < 1 2
B. m = ± 1 2
C. - 1 4 > m < 1 4
D. m = ± 1 4
Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để bất phương trình
(
m
+
1
)
x
2
-
2
(
m
+
1
)
x
+
4
≥
0
(
1
)
có tập nghiệm
S
ℝ
?
A.
m
-
1
B.
-
1
≤...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Cho phương trình
sin
x
+
m
2
3
+
sin
2
x
-
m
2...
Đọc tiếp
Cho phương trình sin x + m 2 3 + sin 2 x - m 2 3 = 2 sin x - m 2 3 . Gọi S = [a;b] là tập hợp tất cả các giá trị thực của tham số m để phương trình trên có nghiệm thực. Tìm giá trị của P = a 2 + b 2
A. P = 162 49
B. P = 49 162
C. P = 4
D. P = 2
Tìm tất cả các giá trị của tham số m để phương trình \(x^2+\sqrt{1-x^2}=m\) có nghiệm là [a; b]
Tính S = a + b
Đặt \(\sqrt{1-x^2}=t\Rightarrow t\in\left[0;1\right]\)
Pt trở thành:
\(1-t^2+t=m\)
Xét hàm \(f\left(t\right)=-t^2+t+1\) trên \(\left[0;1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[0;1\right]\)
\(f\left(0\right)=1\) ; \(f\left(1\right)=1\); \(f\left(\dfrac{1}{2}\right)=\dfrac{5}{4}\)
\(\Rightarrow1\le f\left(t\right)\le\dfrac{5}{4}\Rightarrow\) pt có nghiệm khi \(m\in\left[1;\dfrac{5}{4}\right]\)
Đúng 1
Bình luận (4)
Cho phương trình log 2 x = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực.
A. m ≥ 0
B. m ∈ ℝ
C. m > 0
D. m ∈ ℤ
Đáp án là B
Tập giá trị của hàm số log a x = R
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm:
2
x
2
+
x
+
m
2
−
2
m
0
. A.
m
1
2
.
B. m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm: 2 x 2 + x + m 2 − 2 m = 0 .
A. m = 1 2 .
B. m = 3
C. m = 1
D. m = 3 4 .
Đáp án C
Đặt t = x ≥ 0 , khi đó PT đã cho trở thành 2 t 2 + t + m 2 − 2 m = 0 ⇔ 2 t 2 + t = − m 2 + 2 m
Hàm số y = 2 t 2 + t đồng biến trên 0 ; + ∞ .
Để PT đã cho có nghiệm thì − m 2 + 2 m ≥ y 0 ⇔ − m 2 + 2 m ≥ 1 ⇔ m − 1 2 ≤ 0 ⇔ m = 1
Đúng 0
Bình luận (0)
Cho phương trình log 2 m = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực
A. m ≥ 0
B. m ∈ R
C. m > 0
D. < 0
Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm
x
2
+
4
x
+
y
m
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm x 2 + 4 x + y = m 2 x 2 + x y ( x + 2 ) = 9
A. m ≥ 6
B. - 10 ≤ m ≤ 6
C. m ≤ - 10
D. m ≤ - 10 hoặc m ≥ 6
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm
2
m
cos
x
+
sin
x
2
m
2
+
cos
x
−
sin
x +
3
2
A.
−
1
2
m
1
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm 2 m cos x + sin x = 2 m 2 + cos x − sin x + 3 2
A. − 1 2 < m < 1 2
B. m = ± 1 2
C. − 1 4 < m < 1 4
D. m = ± 1 4
1) Tìm tập nghiệm S của bất phương trình | 2x+1| > x+1
2) Tìm tất cả giá trị của tham số m để bất phương trình -x^2+x-m>0 vô nghiệm
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Đúng 2
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm
x
∈
[
1
;
2
]
.
x
4
+
16
x
4
+
4
(
x
2
+
4
x
2
)
-
12
(
x
-
2
x
)
m
A.
-...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm x ∈ [ 1 ; 2 ] .
x 4 + 16 x 4 + 4 ( x 2 + 4 x 2 ) - 12 ( x - 2 x ) = m
A. - 13 ≤ m ≤ 11
B. - 15 ≤ m ≤ 9
C. - 15 < m < 9
D. - 16 ≤ m ≤ 9
Đáp án là B.
Đặt t = x - 2 x Đạo hàm t , = 1 + 2 x 2 > 0
Do đó t ( 1 ) ≤ t ≤ t ( 2 ) , ∀ x ∈ [ 1 ; 2 ] , suy ra - 1 ≤ t ≤ 1
Ta có x 2 + 4 x 2 = t 2 + 4 , x 4 + 16 x 4 = ( x 2 + 4 x 2 ) 2 - 8 = ( t 2 + 4 ) 2 - 8 = t 4 + 8 t 2 + 8
Phương trình đã cho trở thành
t 4 + 8 t 2 + 8 - 4 ( t 2 + 4 ) - 12 t = m ⇔ t 4 + 4 t 2 - 12 t = m + 8 ( * )
Phương trình đã cho có nghiệm trong đoạn [1;2] khi và chỉ khi phương trình (*) có nghiệm trong [-1;1] Xét hàm số y=f(t)= t 4 + 4 t 2 - 12 t trên [-1;1]
Đạo hàm y , = 4 t 8 + 8 t - 12 , t ∈ ( - 1 ; 1 ) . y , = 4 ( t - 1 ) ( t 2 + t + 3 ) < 0 , ∀ t ∈ ( - 1 ; 1 )
Bảng biến thiên:
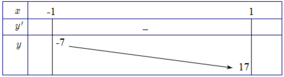
Do đó để phương trình đã cho có nghiệm trên [1;2] thì - 7 ≤ m + 8 ≤ 17 ⇔ - 15 ≤ m ≤ 9
Đúng 0
Bình luận (0)