Cho đa thức f(x) hệ số thực và thỏa điều kiện 2 f x + f 1 - x = x 2 , ∀ x ∈ ℝ . Tìm tất cả các giá trị của tham số thực m để hàm số y = 3 x . f x + m - 1 x + 1 đồng biến trên ℝ
A. m ∈ ℝ
B. m ≥ 10 3
C. m ≤ 1
D. m > 1
bài 1: Cho 2 đa thức P(x) và Q(x) thỏa mãn điều kiện: P(x)=Q(x)+ Q(1-x) vs mọi x thuộc R
Biết rằng các hệ số của đa thức P(x) là các số nguyên ko âm và P(0)=0. Tính P(P(3))
Bài 2: Cho đa thức f(x) là đa thứ bậc 4 có hệ số cao nhất là 1 thỏa mãn; f(1)=3;f(3)=11;f(5)=27
Tính f(-2) + 7*f(6)
Cho đa thức f(x) hệ số thực và thỏa điều kiện 2 f x + f 1 - x = x 2 , ∀ x ∈ ℝ . Tìm tất cả các giá trị của tham số thực m để hàm số y = 3 x f x + m - 1 x + 1 đồng biến trên ℝ
A. m ∈ ℝ
B. m ≥ 10 3
C. m ≤ 1
D. m > 1
Từ giả thiết, thay x bởi x-1 ta được ![]()
Khi đó ta có 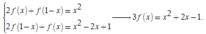
Suy ra ![]()
YCBT ![]()
![]()
Chọn B.
Viết đa thức F(x) thỏa mãn đồng thời các điều kiện sau:
- Bậc của F(x) bằng 3
- Hệ số của x2 bằng hệ số của x và bằng 2
- Hệ số cao nhất của F(x) bằng -6 và hệ số tự do bằng 3.
F(x) = -6x3 + 2x2 + 2x + 3
\(F\left(x\right)=-6x^3+2x^2+2x+3\)
cho f(x) là 1 đa thức bậc 4 có hệ số cao nhất là 1 thỏa mãn điều kiện f(1)=3;f(3)=11;f(5)=27.tính f(-2)+7.f(6)
Xét g(x) = f(x) - x^2 -2
g(x) có bậc 4 và g(1)=g(3)=g(5)=0
Vậy g(x)=(x-1)(x-3)(x-5)(x+a) vì f có hệ số cao nhất là 1
=> f(x) = (x-1)(x-3)(x-5)(x+a) + x^2 +2
f(-2) = -105(a-2) + 6 = 216 -105a
f(6) = 15(a+6) + 38 = 128 +15a
f(-2) + 7f(6) = 216 - 105a + 896 + 105a = 1112
viết đa thức F(x) thỏa mãn đồng thời các điều kiện sau:
a. Bậc của F(x) bằng 3
b. Hệ số của x2 bằng hệ số của x và bằng 2
c. hệ số cao nhất của F(x) bằng -6 và hệ số tự do bằng 3
a: F(x)=ax^3+bx^2+cx+d
b: F(x)=ax^3+2x^2+2x+d
c: f(x) có hệ số cao nhất là -6 và hệ số tự do bằng 3 nên f(x)=-6x^3+2x^2+2x+3
Cho đa thức f(x) bậc bốn thỏa mãn 2 điều kiện sau: f(-1)=0 và f(x)-f(x-1)=x(x+1)(2x+1)
tìm tất cả các đa thức f[x] có hệ số nguyên thõa mãn điều kiện [x+1].f[x]=[x-2].f[x+2] và f[0]=1
tìm tất cả các đa thức f[x] có hệ số nguyên thõa mãn điều kiện [x+1].f[x]=f[x+2].[x-2] và f[0]=1
Tìm tất cả các đa thức f(x) có các hệ số nguyên thỏa mãn điều kiện:
(x+1)*f(x)=(x-2)*f(x+2) và f(0)=1