A = { -10 ; -9 ; -8; ....... ; 5 ; 6 ; 7 }
tính tổng của A ( không cần lời giải , có thể ra đáp số luôn )
Những câu hỏi liên quan
cho a^n= a^10 . (a^2)^10 . (a^3)^10 .......... .(a^10)^10 hỏi n bằng bao nhiêu
Theo đề bài ta có :
\(a^n=a^{10}\cdot\left(a^2\right)^{10}\cdot\left(a^3\right)^{10}...\left(a^{10}\right)^{10}\)
\(\Leftrightarrow a^n=a^{10}\cdot a^{20}\cdot a^{30}...a^{100}\)
\(\Rightarrow a^n=a^{10+20+30+...+100}\)
\(\Rightarrow n=10+20+30+...+100\)
\(\Rightarrow n=550\)
Đáp số : n = 550.
Đúng 0
Bình luận (0)
bài 2: viết thành dạng lũy thừa các tích sau:
a) 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2
b) 10 . 10 . 10 . 10 . 10
c) 8 . 8 . 8 . 6 . 6 . 6 . 7 . 7 . 7
d) a . a . a . a . a . a . a . a . a
e) 10000 . 10 . 10 . 10 . 100
f) 2x . 2x . 2x . 2x . 2x
nhanh nha, mik tick cho
a) 28
b) 105
c) 83 . 63 . 73
d) a9
e) 109
f) 2x5
Đúng 2
Bình luận (0)
Tìm số dư trong phép chia A cho 7 biết A = 10^10 + 10^10^2 + 10^10^3 + ... + 10^10^10
Đặt A=1010+10102+...+10102015A=1010+10102+...+10102015
Dễ thấy 1010≡4(mod7)1010≡4(mod7)
Nên A≡4+410+4102+...+4102014A≡4+410+4102+...+4102014
Dễ chứng minh được 410≡4(mod7)410≡4(mod7)
Nên 410≡4102≡...≡4102015≡4(mod7)410≡4102≡...≡4102015≡4(mod7)
Do đó A≡4.2015≡3(mod7)A≡4.2015≡3(mod7)
Đúng 0
Bình luận (0)
bài 2: viết thành dạng lũy thừa các tích sau:a) 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2b) 10 . 10 . 10 . 10 . 10c) 8 . 8 . 8 . 6 . 6 . 6 . 7 . 7 . 7d) a . a . a . a . a . a . a . a . ae) 10000 . 10 . 10 . 10 . 100f) 2x . 2x . 2x . 2x . 2xnhanh nha, mik tick cho
Đọc tiếp
bài 2: viết thành dạng lũy thừa các tích sau:
a) 2 . 2 . 2 . 2 . 2 . 2 . 2 . 2
b) 10 . 10 . 10 . 10 . 10
c) 8 . 8 . 8 . 6 . 6 . 6 . 7 . 7 . 7
d) a . a . a . a . a . a . a . a . a
e) 10000 . 10 . 10 . 10 . 100
f) 2x . 2x . 2x . 2x . 2x
nhanh nha, mik tick cho
Lời giải:
a. $=2^8$
b. $=10^5$
c. $=8^3.6^3.7^3=(8.6.7)^3=336^3$
d. $=a^9$
e. $=10000.10^3.100=10^4.10^3.10^2=10^{4+3+2}=10^9$
f. $=(2x)^5$
Đúng 2
Bình luận (0)
Bài \(2\)
\(a)\) \(2.2.2.2.2.2.2.2=2^8\)
\(b)\) \(10.10.10.10.10=10^5\)
\(c)\) \(8.8.8.6.6.7.7.7=8^3.6^2.7^3\)
\(d)\) \(a.a.a.a.a.a.a.a.a=a^9\)
\(e)\) \(10000 . 10 . 10 . 10 . 100\)
\(=10^4.10.10.10.10^2=10^9\)
\(f)\) \(2x.2x.2x.2x.2x=\left(2x\right)^5\)
Đúng 1
Bình luận (0)
a) \(2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\)
\(=2^{1+1+1+1+1+1+1+1}\)
\(=2^8\)
b) \(10\cdot10\cdot10\cdot10\cdot10\)
\(=10^{1+1+1+1+1}\)
\(=10^5\)
c) \(8\cdot8\cdot8\cdot6\cdot6\cdot6\cdot7\cdot7\cdot7\)
\(=8^{1+1+1}\cdot6^{1+1+1}\cdot7^{1+1+1}\)
\(=8^3\cdot6^3\cdot7^3\)
\(=\left(8\cdot6\cdot7\right)^3\)
\(=336^3\)
d) \(a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\)
\(=a^{1+1+1+1+1+1+1+1+1}\)
\(=a^9\)
e) \(10000\cdot10\cdot10\cdot10\cdot100\)
\(=10^4\cdot10\cdot10\cdot10\cdot10^2\)
\(=10^{4+1+1+1+2}\)
\(=10^9\)
f) \(2x\cdot2x\cdot2x\cdot2x\cdot2x\)
\(=\left(2x\right)^{1+1+1+1+1}\)
\(=\left(2x\right)^5\)
\(=32x^5\)
Đúng 0
Bình luận (0)
So sánh:
a,A=2009^2010+2009^2009 và B=2010^2010
b,A=10^8+2/10^8-1 và B=10^8/10^8-3
c,A=10^11+1/10^12+1 và B=10^10+1/10^11+1
Mình làm câu a) nha!!!
+) \(A=2009^{2010}+2009^{2009}\)
\(=2009^{2009}.\left(2009+1\right)\)
\(=2009^{2009}.2010\)
+) \(B=2010^{2010}=2010^{2009}.2010\)
Vì \(2010^{2009}>2009^{2009}\)nên \(2010^{2009}.2010>2009^{2009}.2010\)hay \(B>A\)
Vậy \(A< B\)
Hok tốt nha^^
Đúng 0
Bình luận (0)
Câu 21. Viết số có 4 chữ số abcd dưới dạng tổng các lũy thừa của 10 là:
A. 4 3 2 a b c d .10 .10 .10 .10
B. 2 a b c d .10 .10 .1
C. 4 2 a b c d .10 .10 .10
D. 3 2 a b c d
lỗi rồi nhé
Bị lỗi rồi
Hình như sao chép bị lỗi
Mình đăng câu khác nhé
Hai xạ thủ A và B cùng bắn 15 phát đạn, kết quả ghi lại sau đây:
A
6
6
10
9
10
10
7
10
10
9
9
10
10
10
10
B
9
9
8
10
10
8
8
10
8
9
10
8
10
10
9
Điểm trung bình lần lượt của xạ thủ A và B là A. 8; 9 B. 9; 10 C. 8,5 ; 8,6 D. 9,1 ; 9,1
Đọc tiếp
Hai xạ thủ A và B cùng bắn 15 phát đạn, kết quả ghi lại sau đây:
| A | 6 | 6 | 10 | 9 | 10 | 10 | 7 | 10 | 10 | 9 | 9 | 10 | 10 | 10 | 10 |
| B | 9 | 9 | 8 | 10 | 10 | 8 | 8 | 10 | 8 | 9 | 10 | 8 | 10 | 10 | 9 |
Điểm trung bình lần lượt của xạ thủ A và B là
A. 8; 9
B. 9; 10
C. 8,5 ; 8,6
D. 9,1 ; 9,1
Điểm trung bình của xạ thủ A là:
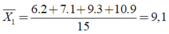
Điểm trung bình của xạ thủ B là:
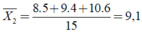
Chọn đáp án D.
Đúng 0
Bình luận (0)
So sánh
a, A= 10^11-1/10^12-1 và B = 10^10+1/10^11+1
b, A= -9/10^2010+-19/10^2011 và B = -9/10^2011+-19/10^2010
Tìm a THUỘC Z BIẾT
a) ( a+3) . (a+10) <0
b) ( a+10) . (a -10) > 0
c) (a+3) . (a +10) . (a-10) >0
d) (a+3) . (a+10) . (a -10) < 0
GIẢI RA NHÉ CÁC BẠN , AI LÀM ĐƯỢC CÂU NÀO ĐÚNG MÌNH TICK CHO OK
GIỎI THÌ CỐ LÀM HẾT NHÉ
Để (a+3)(a+10)<0 thì a+3 và a+10 trái dấu. Nên a+30 và a>-10. a+3<0 và a<-3. =>-10
Đúng 0
Bình luận (0)
15 tháng 2 2022 lúc 21:00
\(a^{30}b^{30}+b^{30}c^{30}+c^{30}a^{30}=3a^{20}b^{20}c^{20} tính A= (1+\dfrac{a^{10}}{b^{10}}).(1+\dfrac{b^{10}}{c^{10}}).(1+\dfrac{c^{10}}{^{10}})\)