Tìm giá trị của a để I = ∫ 0 a 5 x + 7 x 2 + 3 x + 2 d x = 3 ln 2 + 2 ln 3
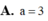
![]()
![]()
![]()
(2/(x+1)-1/(x-1)-5/1-(x^2):2x+1/x^2-1
a)tìm điều kiện của x để giá trị a xác định và cm a=x+2/2x+1
b)tìm giá trị x để a=3
c)tìm giá trị của a với x thỏa mãn x^2-x=0
chỉ mình câu này với
rút gon biểu thức A= x^2+2x/ x^2-4x+4 : ( x+2/x-1/2-x+6-x^2/x^2-2x) với x khác 0,2,-2
rút gọn A
tính giá trị của A biết I 2x +1 I =3
tìm x để A<0 , tìm giá trị x nguyên để A nhận giá trị nguyên , tìm gía trị nhỏ nhất của với x>2
cho biểu thức
A=x^2+2x/2x+10 + x-5/x + 50-5x/2x(x+5)
a', tìm điều kiện xác định va rút gọn A
b, tìm x để A=0 , A=1/4
c, tính giá trị của A khi x=0 , x=2
d, tìm x để A>0 , A<0
e, tìm x để A nhận giá trị nguyên
ĐKXĐ: \(x\ne-5;0\)
\(A=\frac{x^2+2x}{2x+10}+\frac{x-5}{x}+\frac{50-5x}{2x.\left(x+5\right)}\)
\(=\frac{\left(x^2+2x\right).x}{2x.\left(x+5\right)}+\frac{2.\left(x+5\right).\left(x-5\right)}{2x.\left(x+5\right)}+\frac{50-5x}{2x\left(x+5\right)}\)
\(=\frac{x^3+2x^2}{2x\left(x+5\right)}+\frac{2.\left(x^2-25\right)}{2x\left(x+5\right)}+\frac{50-5x}{2x\left(x+5\right)}=\frac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(=\frac{x^3+4x^2-5x}{2x\left(x+5\right)}=\frac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\frac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\frac{x-1}{2}\)
b. \(A=0\Leftrightarrow\frac{x-1}{2}=0\Rightarrow x-1=0\Leftrightarrow x=1\)
\(A=\frac{1}{4}\Leftrightarrow\frac{x-1}{2}=\frac{1}{4}\Leftrightarrow4x-4=2\Leftrightarrow4x-6=0\Leftrightarrow x=\frac{3}{2}\)
c. Với x=0 thì \(A=\frac{0-1}{2}=-\frac{1}{2}\)
Với x=2 thì: \(A=\frac{2-1}{2}=\frac{1}{2}\)
d. \(A>0\Leftrightarrow\frac{x-1}{2}>0\Rightarrow\left(x-1\right).2>0\Rightarrow x-1>0\Leftrightarrow x>1\)
\(A< 0\Leftrightarrow\frac{x-1}{2}< 0\Leftrightarrow\left(x-1\right).2< 0\Leftrightarrow x-1< 0\Leftrightarrow x< 1;x\ne-5,0\)
e. \(A=\frac{x-1}{2}\inℤ\Rightarrow x-1\in Z\Rightarrow x\inℤ\)
Và \(\left(x-1\right)⋮2\Rightarrow x:2dư1\)
Vậy \(A\in Z\Leftrightarrow x\inℤ\)và x chia 2 dư 1
tìm các giá trị của x để :A=5*x+4/x2+1
a)A=0; b)A>0; c)A<0
\(a)\dfrac{5x+4}{x^2+1}=0\)
\(\Rightarrow5x+4=0\)
\(\Rightarrow x=-\dfrac{4}{5}\)
Vậy \(A=0\Leftrightarrow x=-\dfrac{4}{5}\)
\(b)\dfrac{5x+4}{x^2+1}>0\)
Do \(x^2+1>0\forall x\)
\(\Rightarrow5x+3>0\)
\(\Rightarrow x>-\dfrac{4}{5}\)
Vậy \(A>0\Leftrightarrow x>-\dfrac{4}{5}\)
\(c)\dfrac{5x+4}{x^2+1}< 0\)
Do \(x^2+1>0\forall x\)
\(\Rightarrow5x+4< 0\)
\(\Rightarrow x< -\dfrac{4}{5}\)
Vậy \(A< 0\Leftrightarrow x< -\dfrac{4}{5}\)
Cho biểu thức : P = \(\dfrac{\text{x}^{\text{2}}+2x}{2x+10}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
a) Rút gọn biểu thức P
b) Tìm giá trị của x để P = 0
c) Tìm giá trị của x để P > 0, P < 0
a: \(P=\dfrac{x\left(x+2\right)}{2\left(x+5\right)}+\dfrac{x-5}{x}-\dfrac{5x-50}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+2x^2-50-5x+50}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
Tìm giá trị của x để số A=7.x-8:5=0
7.x - 8 : 5 = 0
7.x - 8 = 5
7.x = 13
x = \(\dfrac{13}{7}\)
7.x - 8 : 5 = 0
7x -8 = 0
7x = 8
x = \(\dfrac{8}{7}\)
7.x-8:5=0 7.x-1,6=0 7.x=1,6 x=1,6/7 x=8/35
A=2x/x^2-25+5/5-x-1/x+5 a, tìm giá trị của x để giá trị của biểu thúc A được xác định b,Tìm giá trị nguyên của x để A nhận giá trị nguyên
a) ĐKXĐ: \(x\notin\left\{5;-5\right\}\)
b) Ta có: \(A=\dfrac{2x}{x^2-25}+\dfrac{5}{5-x}-\dfrac{1}{x+5}\)
\(=\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5}{x-5}-\dfrac{1}{x+5}\)
\(=\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{2x-5x-25-x+5}{\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{-4x-20}{\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{-4\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{-4}{x-5}\)
Để A nguyên thì \(-4⋮x-5\)
\(\Leftrightarrow x-5\inƯ\left(-4\right)\)
\(\Leftrightarrow x-5\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{6;4;7;3;9;1\right\}\)(nhận)
Vậy: Để A nguyên thì \(x\in\left\{6;4;7;3;9;1\right\}\)
Bài 1: Cho số hữu tỉ x = a - 5 ( a khác 0 )
Với giá trị nguyên nào của a thì x có giá trị nguyên
Bài 2: Tìm giá trị nguyên của a để các biểu thức sau có giá trị nguyên
A= 3a + 9/a - 4 B= 6a + 5/ 2a - 1
ta thấy rằng 5 phải chia hết cho a tức là
a(U)5=1,-1;5,-5
vậy a 1,-1,5,-5 thì x có giá trị nguyên
Bài 3. Cho biểu thức: \(P=\dfrac{x^2+2x}{2x+20}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
a) Tìm điều kiện xác định của P
b) Rút gọn biểu thức P
c) Tìm giá trị của x để P = 0; P = \(\dfrac{1}{4}\)
d) Tìm giá trị của x để P > 0; P < 0
a) ĐKXĐ: \(x\ne-10;x\ne0;x\ne-5\)
b) \(P=\dfrac{x^2+2x}{2x+20}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^2+2x}{2\left(x+10\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x^2+2x\right)\left(x+5\right)}{2x\left(x+10\right)\left(x+5\right)}+\dfrac{2\left(x-5\right)\left(x+10\right)}{2x\left(x+10\right)\left(x+5\right)}+\dfrac{\left(50-5x\right)\left(x+10\right)}{2x\left(x+5\right)\left(x+10\right)}\)
\(=\dfrac{x^4+7x^3+10x^2+2x^2+10x-100+500-5x^2}{2x\left(x+10\right)\left(x+5\right)}\)
\(=\dfrac{x^4+7x^3+7x^2+10x+400}{2x\left(x+10\right)\left(x+5\right)}\)
c) \(P=0\Rightarrow x^4+7x^3+7x^2+10x+400=0\Leftrightarrow...\)
Số xấu thì câu c, d làm cũng như không. Bạn xem lại đề.
Bài 11: Cho biểu thức A = \(\dfrac{9-3x}{x^2+4x-5}-\dfrac{x+5}{1-x}-\dfrac{x+1}{x+5}\) (với x ≠ -5; x ≠ 1)
a) Rút gọn A b) Tìm các giá trị nguyên của x để A nhận giá trị nguyên
c) Tìm x sao cho A<0 d) Tìm x sao cho |A| = 3
\(a,A=\dfrac{9-3x+x^2+10x+25-x^2+1}{\left(x-1\right)\left(x+5\right)}\\ A=\dfrac{7x+35}{\left(x-1\right)\left(x+5\right)}=\dfrac{7\left(x+5\right)}{\left(x-1\right)\left(x+5\right)}=\dfrac{7}{x-1}\\ b,A\in Z\\ \Leftrightarrow x-1\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ \Leftrightarrow x\in\left\{-6;0;2;8\right\}\left(tm\right)\\ b,A< 0\Leftrightarrow x-1< 0\left(7>0\right)\\ \Leftrightarrow x< 1;x\ne-5\\ c,\left|A\right|=3\Leftrightarrow\dfrac{7}{\left|x-1\right|}=3\Leftrightarrow\left|x-1\right|=\dfrac{7}{3}\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}+1=\dfrac{10}{3}\left(tm\right)\\x=-\dfrac{7}{3}+1=-\dfrac{4}{3}\left(tm\right)\end{matrix}\right.\)