Giá trị của tổng 4+44+444+...+44...4 (tổng đó có 2018 số hạng) bằng
A. 4 9 10 2019 - 10 9 - 2018
B. 4 9 10 2019 - 10 9 + 2018
C. 4 9 10 2018 - 1
D. 40 9 10 2018 - 1 + 2018
Những câu hỏi liên quan
Giá trị của tổng
4
+
44
+
444
+
...
+
44...4
(tổng đó có 2018 số hạng) bằng A.
40
9
10
2018
−
1
+
2018
B.
4
9
10
2018
−...
Đọc tiếp
Giá trị của tổng 4 + 44 + 444 + ... + 44...4 (tổng đó có 2018 số hạng) bằng
A. 40 9 10 2018 − 1 + 2018
B. 4 9 10 2018 − 1
C. 4 9 10 2019 − 10 9 + 2018
D. 4 9 10 2019 − 10 9 − 2018
Đáp án D
Lời giải:
A = 4 9 9 + 99 + ... + 99...9 = 4 9 1 − 1 + 10 − 1 + 10 2 − 1 + .... + 10 2018 − 1 = 4 9 1 + 10 + 10 2 + ... + 10 2018 − 2019 = 4 9 10 2019 − 1 10 − 1 − 2019 = 4 9 10 2019 − 10 9 − 2018
Đúng 0
Bình luận (0)
Giá trị của tổng
4
+
44
+
444
+
...
+
4...4
(tổng đó có 2018 số hạng) bằng: A.
4
9
10
2019
−
10
9
−...
Đọc tiếp
Giá trị của tổng 4 + 44 + 444 + ... + 4...4 (tổng đó có 2018 số hạng) bằng:
A. 4 9 10 2019 − 10 9 − 2018 .
B. 4 9 10 2019 − 10 9 + 2018 .
C. 4 9 10 2018 − 1 .
D. 40 9 10 2018 − 1 + 2018.
Giá trị của tổng
4
+
44
+
444
+
.
.
.
+
4
.
.
.
4
(tổng đó có 2018 số hạng) bằng A.
4
9
10
2019
-
10
9
-...
Đọc tiếp
Giá trị của tổng 4 + 44 + 444 + . . . + 4 . . . 4 (tổng đó có 2018 số hạng) bằng
A. 4 9 10 2019 - 10 9 - 2018
B. 4 9 10 2019 - 10 9 + 2018
C. 4 9 10 2018 - 1
D. 40 9 10 2018 - 1 + 2018
Giá trị của tổng 4+44+444+....+44..4 (tổng đó có 2018 số hạng)
Đọc tiếp
Giá trị của tổng 4+44+444+....+44..4 (tổng đó có 2018 số hạng)
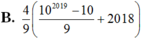
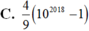
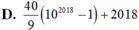
Tính giá trị của tổng \(4+44+444+...+44...4\)( biết tổng có 2018 số hạng )
Lời giải:
Đặt \(\underbrace{11...1}_{n}=a\Rightarrow 9a+1=10^n\Rightarrow a=\frac{10^n-1}{9}\Rightarrow \underbrace{44...4}_{n}=4a=\frac{4}{9}(10^n-1)\)
Thay $n=1,2,...,2018$ và đặt tổng cần tính là $T$
Khi đó:
\(T=\frac{4}{9}(10^1-1)+\frac{4}{9}(10^2-1)+\frac{4}{9}(10^3-1)+...+\frac{4}{9}(10^{2018}-1)\)
\(=\frac{4}{9}(10+10^2+10^3+...+10^{2018}-2018)\)
\(10T=\frac{4}{9}(10^2+10^3+...+10^{2019}-20180)\)
Trừ theo vế:
\(9T=10T-T=\frac{4}{9}(10^{2019}-20180-10+2018)=\frac{4}{9}(10^{2019}-18172)\)
\(\Rightarrow T=\frac{4(10^{2019}-18172)}{81}\)
B=4+44+444+...+444..4( 444..4 có 10 chữ số 4)
hãy tính tổng B
Cho tổng sau: 4 + 44 + 444 + 4444 +.......+ 444....44(2000 chữ số 4)
Tìm 4 chữ số tận cùng của tổng trên.
Ta thấy
Số thứ nhất có một chữ số 4Số thứ hai có hai chữ số 4Số thứ ba có ba chữ số 4Tương tự : 4444....44( 2000 chữ số bốn) => là số thứ 2000đáp án tổng trên là........abcd
d= 4*2000=.....0c=4*1999=.........6( nhớ 3)b= 4*1998=........2 cộng vói nhớ 3 trên =5(nhớ 3)a=4*1997=........8 công với nhớ 3 trên =1=> abcd=1560
Đúng 0
Bình luận (0)
4 chữ số tận cùng của tổng trên là 8888
Đúng 0
Bình luận (0)
Đặt tổng đó =A
A=4(1+11+111+1111+...+111...11(2000 chữ số 1))
Ta thấy cứ tổng của 10 số hạng có tận cùng bằng 1 thì tận cùng bằng 0. Mặt khác, A có 2000 số hạng có tận cùng bằng 1
=>A có tận cùng =0
Nói kiểu này thì hơi khó hiểu nhưng không còn cách nào khác nên mong bạn tự hiểu!!
Đúng 0
Bình luận (0)
Biết 4.4 < x < 4+44+444 (x thuộc N ) . Tính tổng tất cả các giá trị của x
4.4 < x < 4+44+444
=> 16 < x < 492
=> x={17;18;..;492}
Tổng của x là : [(492-17):1+1].[(492+17):2]=476.254,5=121142
Đúng 0
Bình luận (0)
Ta có 4*4 < x < 4+44+444
hay 16 < x < 492
\(\Rightarrow x\in\left\{17,18,...,491\right\}\)
Số số hạng của tập hợp trên là
( 491 - 17 ) : 1 + 1 = 475 (số)
Tổng là
( 491 + 17 ) *475 / 2 = 120650
Đúng 0
Bình luận (0)
a) A = 9+99+999+...+99...9 (99...9 có 10 chữ số 9)
b) B=1+11+111+...+11...1 (11...1 có 10 chữ số 1)
c) C= 4+44+444+...+44...4 (44...4 có 10 chữ số 4)
Tớ hướng dẫn câu A thui, mấy câu còn lại làm tương tự
A = 9 + 99 + 999 + ... + 99...9(10 chữ số 9)
Ta để ý: 9 = 101 - 1
99 = 102 - 1
999 = 103 - 1
.....
99..9(10 chữ số 9) = 1010 - 1
Công thức tổng quát: \(\overline{aa...aa}=\frac{a}{9}\left(10^n-1\right)\) với n là số chữ số của aa..aa
Suy ra tổng A = 101 + 102 + 103 + ... + 1010 - 10
=> A = 11111111110 - 10 = 111111111100
B,C làm tương tự với công thức tổng quát
Đúng 0
Bình luận (0)