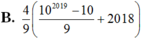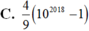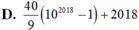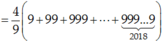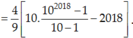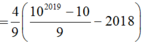Các câu hỏi tương tự
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng A. 21 B. 42 C.20 D. 17
Đọc tiếp
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C.20
D. 17
Tính tổng
S
C
2018
1009
+
C
2018
1010
+
C
2018
1011
+
.
.
.
+
C
2018
2018
(trong tổng đó, các số hạng có dạng
C
2018
k
với k nguyên dương nhận giá trị liên tục...
Đọc tiếp
Tính tổng S = C 2018 1009 + C 2018 1010 + C 2018 1011 + . . . + C 2018 2018 (trong tổng đó, các số hạng có dạng C 2018 k với k nguyên dương nhận giá trị liên tục từ 1009 đến 2018)
A. S= 2 2018 - C 2018 1009
B. S= 2 2017 + 1 2 C 2018 1009
C. S= 2 2017 - 1 2 C 2018 1009
D. S= 2 2017 - C 2018 1009
Tình tổng
S
C
2018
1009
+
C
2018
1010
+
C
2018
1011
+
.
.
.
+
C
2018
2018
(trong tổng đó, các số hạng có dạng
C
2018
k
với k nguyên dương nhận giá...
Đọc tiếp
Tình tổng S = C 2018 1009 + C 2018 1010 + C 2018 1011 + . . . + C 2018 2018
(trong tổng đó, các số hạng có dạng C 2018 k với k nguyên dương nhận giá trị liên tục từ 1009 đến 2018)
A. S = 2 2018 - C 2018 1009
B. S = 2 2017 + 1 2 C 2018 1009
C. S = 2 2017 - 1 2 C 2018 1009
D. S = 2 2017 - C 2018 1009
Tính tổng
S
C
2018
1009
+
C
2018
1010
+
C
2018
1011
+
.
.
.
+
C
2018
2018
(trong tổng đó, các số hạng có dạng
C
2018
k
với k nguyên dương nhận giá trị liên tục...
Đọc tiếp
Tính tổng S = C 2018 1009 + C 2018 1010 + C 2018 1011 + . . . + C 2018 2018 (trong tổng đó, các số hạng có dạng C 2018 k với k nguyên dương nhận giá trị liên tục từ 1009 đến 2018).
![]()
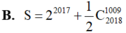
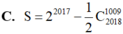
![]()
Ba số có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, hoặc là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng để tổng của chúng là 820?
Cho cấp số cộng
(
u
n
)
có u2013 + u6 1000. Tổng 2018 số hạng đầu tiên của cấp số cộng đó là A. 1009000 B. 100800 C. 1008000 D. 100900
Đọc tiếp
Cho cấp số cộng ( u n ) có u2013 + u6 = 1000. Tổng 2018 số hạng đầu tiên của cấp số cộng đó là
A. 1009000
B. 100800
C. 1008000
D. 100900
6) cho dãy số có các số hạng đầu tiên là 8,15,22,29,36,.. số hạng tổng quát của dãy số là7) cho dãy số left(u_nright) với u_ndfrac{2n+5}{5n-4} với mọi n ϵ N* cho biết số hạng thứ n là dfrac{7}{12}, giá trị của n là8) cho dãy số left(u_nright) với u_ndfrac{2n}{n^2+1} với mọi n ϵ N* số dfrac{9}{41} là số hạng thứ bao nhiêu trong dãy số9) trong các dãy số left(u_nright) cho bởi số hạng tổng quát u_n sau, dãy số nào là dãy số tăngA.u_nleft(dfrac{2}{3}right)^nB. u_ndfrac{n}{n+1}C. u_ndfrac{2}{n.left...
Đọc tiếp
6) cho dãy số có các số hạng đầu tiên là 8,15,22,29,36,.. số hạng tổng quát của dãy số là
7) cho dãy số \(\left(u_n\right)\) với \(u_n=\dfrac{2n+5}{5n-4}\) với mọi n ϵ N* cho biết số hạng thứ n là \(\dfrac{7}{12}\), giá trị của n là
8) cho dãy số \(\left(u_n\right)\) với \(u_n=\dfrac{2n}{n^2+1}\) với mọi n ϵ N* số \(\dfrac{9}{41}\) là số hạng thứ bao nhiêu trong dãy số
9) trong các dãy số \(\left(u_n\right)\) cho bởi số hạng tổng quát \(u_n\) sau, dãy số nào là dãy số tăng
A.\(u_n=\left(\dfrac{2}{3}\right)^n\)
B. \(u_n=\dfrac{n}{n+1}\)
C. \(u_n=\dfrac{2}{n.\left(n+1\right)}\)
D. \(u_n=\dfrac{n+1}{n}\)
10) trong các dãy số \(\left(u_n\right)\) cho bởi số hạng tổng quát \(u_n\) sau, dãy số nào là dãy số giảmA. \(u_n=3^n\)B. \(u_n=\dfrac{n-3}{n+1}\)C. \(u_n=\dfrac{n+4}{n+2}\)D. \(u_n=n^4+2\)Cho cấp số cộng có công sai d=-3 và u22 + u32+ u42 đạt giá trị nhỏ nhất. Tính tổng S100 của 100 số hạng đầu tiên của CSC đó.
Một cấp số nhân dương có 4 số hạng, công bội q bằng 1/4 lần số hạng thứ nhất, tổng của hai số hạng đầu bằng 24. Tìm tích các số hạng cấp số nhân đó?
A. 2
B. 1
C. 4096
D. 262144