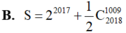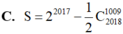Các câu hỏi tương tự
Tính tổng
S
C
2018
1009
+
C
2018
1010
+
C
2018
1011
+
.
.
.
+
C
2018
2018
(trong tổng đó, các số hạng có dạng
C
2018
k
với k nguyên dương nhận giá trị liên tục...
Đọc tiếp
Tính tổng S = C 2018 1009 + C 2018 1010 + C 2018 1011 + . . . + C 2018 2018 (trong tổng đó, các số hạng có dạng C 2018 k với k nguyên dương nhận giá trị liên tục từ 1009 đến 2018)
A. S= 2 2018 - C 2018 1009
B. S= 2 2017 + 1 2 C 2018 1009
C. S= 2 2017 - 1 2 C 2018 1009
D. S= 2 2017 - C 2018 1009
Tình tổng
S
C
2018
1009
+
C
2018
1010
+
C
2018
1011
+
.
.
.
+
C
2018
2018
(trong tổng đó, các số hạng có dạng
C
2018
k
với k nguyên dương nhận giá...
Đọc tiếp
Tình tổng S = C 2018 1009 + C 2018 1010 + C 2018 1011 + . . . + C 2018 2018
(trong tổng đó, các số hạng có dạng C 2018 k với k nguyên dương nhận giá trị liên tục từ 1009 đến 2018)
A. S = 2 2018 - C 2018 1009
B. S = 2 2017 + 1 2 C 2018 1009
C. S = 2 2017 - 1 2 C 2018 1009
D. S = 2 2017 - C 2018 1009
Giá trị của tổng 4+44+444+....+44..4 (tổng đó có 2018 số hạng)
Đọc tiếp
Giá trị của tổng 4+44+444+....+44..4 (tổng đó có 2018 số hạng)

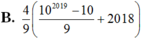
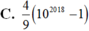
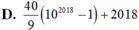
Giá trị của
A
1
1
!
.
2018
!
+
1
2
!
.
2017
!
+
1
3
!
.
2016
!
+
.
.
....
Đọc tiếp
Giá trị của
A = 1 1 ! . 2018 ! + 1 2 ! . 2017 ! + 1 3 ! . 2016 ! + . . . + 1 1008 ! . 1011 ! + 1 1009 ! . 1010 ! bằng
A. 2 2017 - 1 2018 !
B. 2 2017 2018 !
C. 2 2017 2019 !
D. 2 2018 - 1 2019 !
Gọi S là tập các số nguyên của a sao cho
l
i
m
4
n
2
+
2017
n
-
2018
-
a
n
có giá trị hữu hạn. Tính tổng các phần tử của S. A. S 4 B. S 0 C. S 2 D. S 1
Đọc tiếp
Gọi S là tập các số nguyên của a sao cho l i m 4 n 2 + 2017 n - 2018 - a n có giá trị hữu hạn. Tính tổng các phần tử của S.
A. S = 4
B. S = 0
C. S = 2
D. S = 1
Gọi S là tập các số nguyên của a sao cho
l
i
m
4
n
2
+
2017
n
-
2018
-
a
n
có giá trị hữu hạn. Tính tổng các phần tử của S. A. S 4 B. S 0 C. S 2 D. S 1
Đọc tiếp
Gọi S là tập các số nguyên của a sao cho l i m 4 n 2 + 2017 n - 2018 - a n có giá trị hữu hạn. Tính tổng các phần tử của S.
A. S = 4
B. S = 0
C. S = 2
D. S = 1
Cho cấp số cộng
(
u
n
)
có u2013 + u6 1000. Tổng 2018 số hạng đầu tiên của cấp số cộng đó là A. 1009000 B. 100800 C. 1008000 D. 100900
Đọc tiếp
Cho cấp số cộng ( u n ) có u2013 + u6 = 1000. Tổng 2018 số hạng đầu tiên của cấp số cộng đó là
A. 1009000
B. 100800
C. 1008000
D. 100900
Cho 2018 số tự nhiên liên tiếp 1, 2, 3, …,2018. Chọn ngẫu nhiên ba số tự nhiên từ các số đã cho. Tính xác suất để chọn được ba số có một số là trung bình cộng của hai số còn lại A.
3
4034
B.
5
4034
C.
7
4034
D.
9
4034
Đọc tiếp
Cho 2018 số tự nhiên liên tiếp 1, 2, 3, …,2018. Chọn ngẫu nhiên ba số tự nhiên từ các số đã cho. Tính xác suất để chọn được ba số có một số là trung bình cộng của hai số còn lại
A. 3 4034
B. 5 4034
C. 7 4034
D. 9 4034
Tìm nghiệm âm lớn nhất của phương trình
\(\tan^{2018}x + \cot^{2018}x = 2\sin^{2017} (x+ \frac{\pi} {4})\)
có dạng \(\frac{\pi a}{b}\)với a,b là các số nguyên, a<0 và a,b nguyên tố cùng nhau. Tính S = a + b