Kí hiệu z 1 , z 2 , z 3 và z 4 là bốn nghiệm phức của phương trình ( z 2 - 1 ) 2 = 2 z 2 + 46 . Tính tổng M = z 1 ¯ + z 2 + z 3 ¯ + z 4 .
Những câu hỏi liên quan
Cho các số phức z thỏa mãn |z2 + 4| 2|z|. Kí hiệu M max|z| và m min|z|. Tìm module của số phức w M + m?
Đọc tiếp
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
Chọn A.
Ta có 
Giải bất phương trình trên với ẩn |z| ta được:
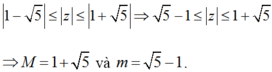
Vậy 
Đúng 0
Bình luận (0)
Chọn kí hiệu "∈", "∉" thích hợp cho ?:
a) - 3 ? \(\mathbb{Z}\);
b) 0 ? \(\mathbb{Z};\)
c) 4 ? \(\mathbb{Z};\)
d) - 2 ? \(\mathbb{N}.\)
a) -3 ∈ Z
b) 0 ∈ Z
c) 4 ∈ Z
d) -2 ∉ N
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
điền các kí hiệu ∈;∉;⊂∈;∉;⊂ thích hợp vào chỗ trống:
a) 3......Z b) -3.......N c) 1.....N d) N.....Z e) 1; -2..........Z
a) \(3\in Z\)
b) \(-3\notin N\)
c) \(1\in N\)
d) \(N\subset Z\)
e) \(1;-2\in Z\)
Đúng 1
Bình luận (0)
a: \(3\in Z\)
b: \(-3\notin N\)
c: \(1\in N\)
d: \(N\subset Z\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
6 tháng 7 2021 lúc 20:51
bài 1 điền (e,e ko thuộc,c) thích hợp vào ...
a)-9...N -9...z -9...Q
b)-8/9...N -8/9...Z -8/9...Q N...Z...Q
bài 2 diền các kí hiệu N Z Q vào ...
1.11e... 2. 1/5e...
3.-26e... 4.-3/4e...
Bài 1:
a) \(-9\notin N\)
\(-9\in Z\)
\(-9\in Q\)
b) \(-\dfrac{8}{9}\notin N\)
\(-\dfrac{8}{9}\notin Z\)
\(-\dfrac{8}{9}\in Q\)
\(N\subset Z\subset Q\)
Đúng 3
Bình luận (0)
điền các kí hiệu \(\in;\notin;\subset\) thích hợp vào chỗ trống:
a) 3......Z b) -3.......N c) 1.....N d) N.....Z e) 1; -2..........Z
a) 3 ∈ Z
b) -3 ∉ N
c) 1 ∈ N
d) N ⊂ Z
e) 1;-2 ∈ Z
Đúng 1
Bình luận (0)
19 tháng 6 2015 lúc 15:23
Kí hiệu này là kí hiệu của tập hợp nào?Z+ và Z-
Z+ là tập hợp số nguyên dương, Z- là tập hợp số nguyên âm
Đúng 0
Bình luận (0)
Z+ là tập hợp các số nguyên dương
Z- là tập hợp các số nguyên âm
Đúng 0
Bình luận (0)
Điền kí hiệu thích hợp vào chỗ chấm :
1) Z+ .... Z
2) N .... Z
3) Z- ... Z+
Chọn kí hiệu "∈", " ∉" thích hợp cho chỗ chấm.
a) -3 ..... N
b) 5 ....... Z
c) 0 ....... Z
d) 1 ....... N
e) -7 ...... Z
f) 0 ........ N
g) -1 ...... N
h) -10 ..... Z
a) - 3 ∉ N
b) 5 ∈ Z
c) 0 ∈ Z
d) 1 ∈ N
e) - 7 ∈ Z
f) 0 ∈ N
g) - 1 ∉ N
h) - 10 ∈ Z
Đúng 3
Bình luận (0)
6 tháng 7 2021 lúc 21:12
bài 2 diền các kí hiệu N Z Q vào ...
1.11e... 2. 1/5e...
3.-26e... 4.-3/4e...