Trong mặt phẳng Oxy , đường thẳng d : a x + b y + c = 0 , a 2 + b 2 ≠ 0 . Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng d ?
A. n → = a ; - b
B. n → = b ; a
C. n → = b ; - a
D. n → = a ; b
Những câu hỏi liên quan
1. Trong mặt phẳng toạ độ oxy, cho 2 đường thẳng delta :x+2y+40 và d: 2x-y+30. Đường tròn tâm I thuộc d cắt Ox tại A và B, cắt trục Oy tại C và D sao cho ABCD2. Tính khoảng cách từ điểm I đến đường thăng delta2. trong mặt phẳng toạ độ oxy, cho tứ giác ABCD với AB:3x-4y+40, BC: 5+12y-520, CD: 5x-12y-40, AD:3x+4y-120. tìm điểm I nằm trong tứ giác ABCD sao cho d(I, AB)d(I,BC)d(I,CD)d(I,DA)
Đọc tiếp
1. Trong mặt phẳng toạ độ oxy, cho 2 đường thẳng delta :x+2y+4=0 và d: 2x-y+3=0. Đường tròn tâm I thuộc d cắt Ox tại A và B, cắt trục Oy tại C và D sao cho AB=CD=2. Tính khoảng cách từ điểm I đến đường thăng delta
2. trong mặt phẳng toạ độ oxy, cho tứ giác ABCD với AB:3x-4y+4=0, BC: 5+12y-52=0, CD: 5x-12y-4=0, AD:3x+4y-12=0. tìm điểm I nằm trong tứ giác ABCD sao cho d(I, AB)=d(I,BC)=d(I,CD)=d(I,DA)
Trong mặt phẳng Oxy, tìm điểm M(a;b) (a>0) thuộc đường thẳng d: x=3+t; y=2+t và cách đường thẳng đenta: 2x-y-3=0 một khoảng 2√5
M thuộc d nên tọa độ có dạng:
\(M\left(t+3;t+2\right)\) với \(t>-3\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|2\left(t+3\right)-\left(t+2\right)-3\right|}{\sqrt{2^2+\left(-1\right)^2}}=2\sqrt{5}\)
\(\Leftrightarrow\left|t+1\right|=10\Rightarrow\left[{}\begin{matrix}t=9\\t=-11\left(l\right)\end{matrix}\right.\)
\(\Rightarrow M\left(12;11\right)\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt phẳng
(
α
)
:
2
x
+
y
-
2
z
-
2
0
, đường thẳng
d
:
x
+
1
1
y
+
2
2
z
+...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 , đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A(1/2; 1; 1). Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng Oxy tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 / 3
B. 7 / 2
C. 21 / 2
D. 3 / 2
Trong không gian Oxyz, cho mặt phẳng
(
α
)
:
2
x
+
y
-
2
z
-
2
0
đường thẳng
d
:
x...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 3
B. 7 2
C. 21 2
D. 3 2
Đáp án B
Phương pháp:
thay tọa độ điểm B vào phương trình ( α ) => 1 phương trình 2 ẩn a, b.
Sử dụng công thức tính khoảng cách
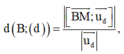
lập được 1 phương trình 2 ẩn chứa a, b.
+) Giải hệ phương trình tìm a,b => Toạ độ điểm B => Độ dài AB.
Dế thấy
Ta có
Lại có
Đường thẳng d đi qua M(0;0;-1), có u → = ( 1 ; 2 ; 2 )
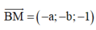
Do đó
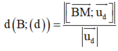
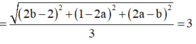
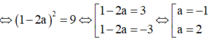
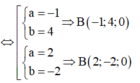
Vậy AB = 7 2
Đúng 0
Bình luận (0)
21 tháng 2 2022 lúc 21:35
Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ
biến đường thẳng Δ: x - y -1 = 0 thành đường thẳng Δ' có phương trình là
A.x - y - 1 = 0 .
B. x + y - 1 = 0 .
C. x - y - 2 = 0 .
D. x + y + 2 = 0 .
Trong mặt phẳng Oxy, cho điểm A(1;2), B(2;4), C(−1;3) và đường thẳng (d) : x + y - 5 = 0 và đường tròn (C) : ((x - 2) ^ 2) + (y + 1) ^ 2 = 4 . a. Tìm ảnh của vec A qua phép tịnh tiến theo vec v = (3; 1) . b. Tìm đường thẳng (d') là ảnh của đường thẳng (d) qua phép tịnh tiến theo a = 3i - 2j C. Tìm đường tròn (C') là ảnh của đường tròn (C) qua phép tịnh tiến theo AB . d. Tìm vec u, biết T vec u (B) = C
a: Ảnh của A là:
x=1+3=4 và y=2+1=3
b: (d') là ảnh của (d) qua phép tịnh tiến vecto a=(3;-2)
=>(d'): x+y+c=0
Lấy B(1;4) thuộc (d)
=>B'(4;2)
Thay x=4 và y=2 vào (d'), ta được:
c+4+2=0
=>c=-6
d: Theo đề,ta có:
2+x=-1 và 4+y=3
=>x=-3 và y=-1
=>vecto u=(-3;-1)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt phẳng
α
:
2
x
+
y
-
2
z
-
2
0
, đường thẳng
d
:
x
+
1
2
y
+
2
2
z
+...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng α : 2 x + y - 2 z - 2 = 0 , đường thẳng d : x + 1 2 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng α , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 2
B. 21 2
C. 7 3
D. 3 2
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: x-y-6 = 0 và hai điểm A (6;4), B (4;0). Viết phương trình đường tròn (C) có tâm thuộc d và đi qua hai điểm A,B
(x-x0)^2+(y-y0)^2=R^2
I(x;x-6)
=> (x-6)^2+(x-6-4)^2=R^2
(x-4)^2+(x-6)^2=R^2
=> x^2-12x+36+x^2-20x+100=x^2-8x+16+x^2-12x+36
=>12x=84
=>x=7
=>R^2=10
`=>(7-x0)^2+(1-y0)^2=10`
Đúng 0
Bình luận (0)
a) Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có đỉnh A(3;5), đường thẳng BC:x+y-2=0. Biết điểm E(6;0) thuộc cạnh CD. Tính diện tích hình chữ nhật ABCD.
b) Trong mặt phẳng Oxy, tìm tọa độ điểm M thuộc đường thẳng d:{x=1+t và y=2-3t sao cho khoảng cách từ điểm M đến đường thẳng đenta: 3x+4y+5=0 bằng 4.
a/ CD qua E và vuông góc BC nên pt có dạng:
\(1\left(x-6\right)-1\left(y-0\right)=0\Leftrightarrow x-y-6=0\)
Ta có: \(AB=d\left(A;BC\right)=\frac{\left|3+5-2\right|}{\sqrt{1^2+1^2}}=3\sqrt{2}\)
\(AD=d\left(A;CD\right)=\frac{\left|3-5-6\right|}{\sqrt{1^2+\left(-1\right)^2}}=4\sqrt{2}\)
\(\Rightarrow S_{ABCD}=AB.AD=24\)
b/ Do M thuộc d nên tọa độ có dạng: \(M\left(1+t;2-3t\right)\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=4\Leftrightarrow\frac{\left|3\left(1+t\right)+4\left(2-3t\right)+5\right|}{\sqrt{3^2+4^2}}=4\)
\(\Leftrightarrow\left|16-9t\right|=20\Rightarrow\left[{}\begin{matrix}16-9t=20\\16-9t=-20\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}t=-\frac{4}{9}\\t=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}M\left(\frac{5}{9};\frac{10}{3}\right)\\M\left(5;-10\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
trong mặt phẳng oxy, cho đường thẳng denta : ax+by +c=0 (a,b,c thuộc N, a<= 4) vuông góc với đường thẳng d : 3x-y+4 = 0 và denta cách A(1;2) một khoảng căn 10
xác định T = a+b+c