Trên mặt phẳng tọa độ 0xy cho 3 điểm \(A\left(\sqrt{a};-37\right)\) \(;\)\(B\left(-5;20\right)\) ; \(C\left(7;-16\right)\) thẳng hàng.
Khi đó \(a\) bằng.
Nêu cả cách giải nhé
Những câu hỏi liên quan
câu 1a) A4sqrt{24}-3sqrt{54}+5sqrt{6}-sqrt{150}b) Bsqrt{14+4sqrt{10}}-dfrac{1}{sqrt{10}+3}câu 2 trong mặt phẳng tọa độ 0xy cho đường thẳng (d1): y2x và đường thẳng (d2): y-x+2a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độb) cho đường thẳng (d3): yax+b. xác định a,b biết rằng đường thẳng (d3) song song với đường thẳng (d2), đồng thời cắt đường thẳng (d1) tại điểm có hoành độ bằng 1
Đọc tiếp
câu 1
a) \(A=4\sqrt{24}-3\sqrt{54}+5\sqrt{6}-\sqrt{150}\)
b) \(B=\sqrt{14+4\sqrt{10}}-\dfrac{1}{\sqrt{10}+3}\)
câu 2 trong mặt phẳng tọa độ 0xy cho đường thẳng (d1): y=2x và đường thẳng (d2): y=-x+2
a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ
b) cho đường thẳng (d3): y=ax+b. xác định a,b biết rằng đường thẳng (d3) song song với đường thẳng (d2), đồng thời cắt đường thẳng (d1) tại điểm có hoành độ bằng 1
Câu 1:
a: \(A=4\sqrt{24}-3\sqrt{54}+5\sqrt{6}-\sqrt{150}\)
\(=4\cdot2\sqrt{6}-3\cdot3\sqrt{6}+5\sqrt{6}-5\sqrt{6}\)
\(=8\sqrt{6}-9\sqrt{6}=-\sqrt{6}\)
b: \(B=\sqrt{14+4\cdot\sqrt{10}}-\dfrac{1}{\sqrt{10}+3}\)
\(=\sqrt{10+2\cdot\sqrt{10}\cdot2+4}-\dfrac{\left(\sqrt{10}-3\right)}{10-9}\)
\(=\sqrt{\left(\sqrt{10}+2\right)^2}-\sqrt{10}+3\)
\(=\sqrt{10}+2-\sqrt{10}+3=5\)
Câu 2:
a:
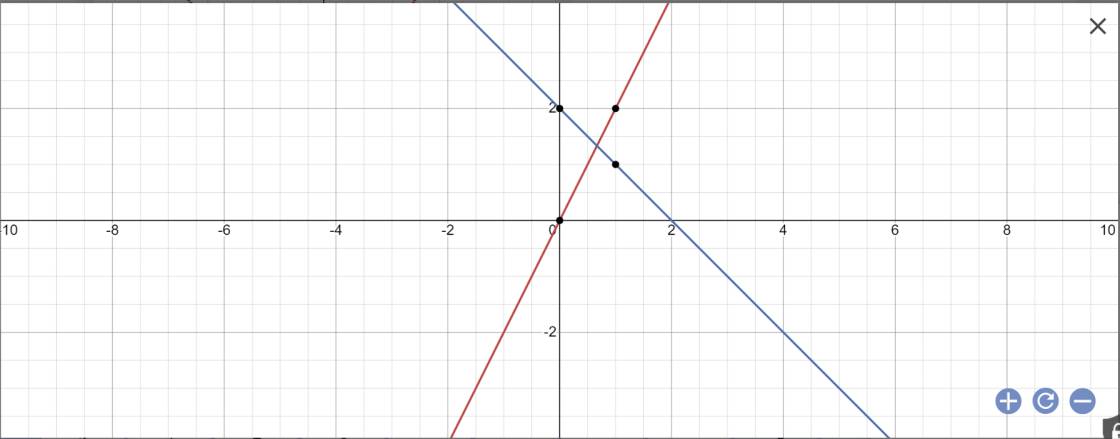
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
b-1=2
=>b=3
vậy: (d3): y=-x+3
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ 0xy ,cho tam giác ABC vuông tại B , BC=2BA .Gọi e ,f lần lượt là trung điểm của BC , AC . Trên tia đối của tia fe lấy điểm m sao cho Fm=3FE .Biết điểm m có tọa độ (5;-1) , đường thẳng AC có phương trình 2X+2y-3=0, điểm A có hoành đọ là số nguyên . Xác định tọa độ các đỉnh của tam giác ABc
trong mặt phẳng 0xy cho A(-1;2)
a) viết ptdt (d) đi qua A và có hệ số góc là -3 vẽ (d)
b) viết ptdt (d1) đi qua M( 2;3) và N(4;5)
c) tìm tọa độ giao điểm (d) và (d1)
a: Vì hệ số góc là -3 nên a=-3
Vậy: (d): y=-3x+b
THay x=-1 và y=2 vào (d), ta được: b+3=2
hay b=-1
Đúng 0
Bình luận (0)
Cho hàm số yleft(m-1right)x^2 left(mne1right) có đồ thị là parabol (P)a, Xác định m để (P) đi qua điểm Aleft(-sqrt{3};1right)b, Với giá tị m vừa tìm được ở trên, hãy; i, Vẽ (P) trên mặt phẳng tọa độ ii, Trong các điểm A(1;1), Bleft(-1;dfrac{1}{3}right) và C(15;-75), điểm nào thuộc (P), điểm nào không thuộc (P) ? iii, Tìm các điểm trên (P) có hoành độ bằng 1 iv, Tìm các điểm trên (P) có tung độ gấp đôi hoành độ
Đọc tiếp
Cho hàm số \(y=\left(m-1\right)x^2\) \(\left(m\ne1\right)\) có đồ thị là parabol (P)
a, Xác định m để (P) đi qua điểm \(A\left(-\sqrt{3};1\right)\)
b, Với giá tị m vừa tìm được ở trên, hãy;
i, Vẽ (P) trên mặt phẳng tọa độ
ii, Trong các điểm A(1;1), B\(\left(-1;\dfrac{1}{3}\right)\) và C(15;-75), điểm nào thuộc (P), điểm nào không thuộc (P) ?
iii, Tìm các điểm trên (P) có hoành độ bằng 1
iv, Tìm các điểm trên (P) có tung độ gấp đôi hoành độ
Câu 1: Trong mặt phẳng 0xy cho A(2;4) B=(-1;4) C=(-5;1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A. . ( -8;1 ) B. . ( 6;7) C. . (-2; 1) D. .( 8;1)
Trong mặt phẳng 0xy cho A(-1;2)
a)Viết phương trình đường thẳng (d) đi qua A và có hệ số góc là -3. Vẽ (d)
b)Viết phương trình đường thẳng (d1) đi qua M( 2;3) và N(4;5)
c)Tìm tọa độ giao điểm (d) và (d1)
a: Vì (d) có hệ số góc là -3 nên a=-3
Vậy: (d): y=-3x+b
Thay x=-1 và y=2 vào (d), ta được:
b+3=2
hay b=-1
Đúng 0
Bình luận (1)
\(a,\) Gọi \(\left(d\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}-a+b=2\\a=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=-1\end{matrix}\right.\Leftrightarrow\left(d\right):y=-3x-1\)
\(b,\) Gọi \(\left(d_1\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}2a+b=3\\4a+b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\Leftrightarrow\left(d_1\right):y=x+1\)
\(c,PTHDGD:-3x-1=x+1\Leftrightarrow x=-\dfrac{1}{2}\Leftrightarrow y=\dfrac{1}{2}\Leftrightarrow B\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\\ \text{Vậy }B\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\text{ là giao 2 đths}\)
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
a)
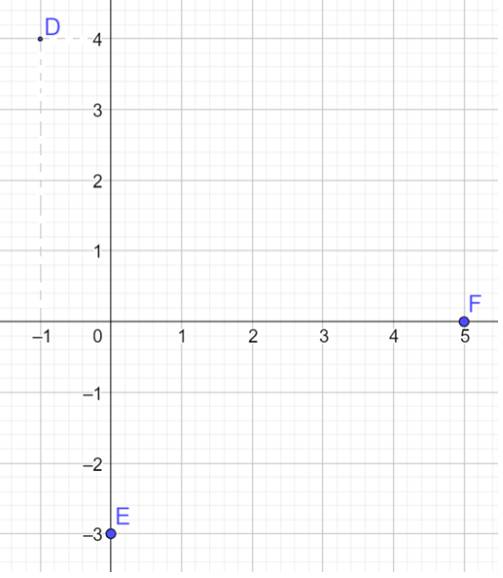
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
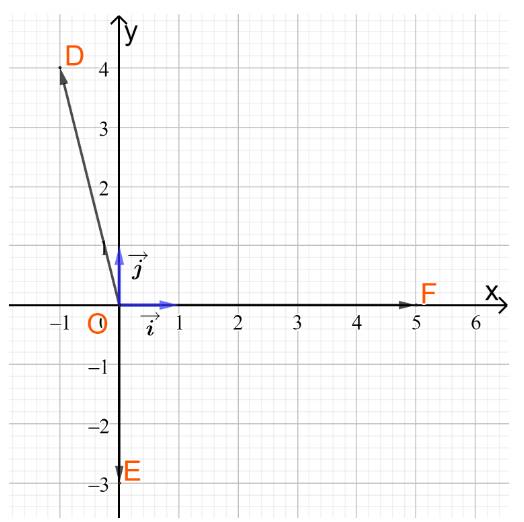
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ 0xy , cho điểm A(4;-3) va B(4;1) và đường thẳng d: x+6y=0 viết PT đường tròn C đi qua A,B sao cho tiếp tuyến của đường tròn tại A và B cắt nhau tại một điểm thuộc d
Cho mặt phẳng \(\left(P\right):x+y+z-3=0\) và điểm \(A\left(1;2;-1\right)\)
Tìm tọa độ điểm A' là hình chiếu của A trên (P) và tọa độ A" đối xứng với A qua (P)
Mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow{p}=\left(1;1;1\right)\), ta có A' là hình chiếu của A trên (P) khi và chỉ khi \(\begin{cases}A'\in\left(P\right)\\AA'\perp\left(P\right)\end{cases}\)
Gọi \(A'\left(x;y;z\right)\) là hình chiếu của A trên (P). Khi đó, ta có hệ phương trình :
\(\begin{cases}x+y+z-3=0\\\frac{x-1}{1}=\frac{y-1}{1}=\frac{z-1}{1}\end{cases}\)
Giải hệ thu được :
\(z=-\frac{2}{3};x=\frac{4}{3};y=\frac{7}{3}\)
Vậy A' cần tìm là \(A'\left(\frac{4}{7};\frac{7}{3};-\frac{2}{3}\right)\)
Nếu A" là điểm đối xứng với A qua mặt phẳng (P) thì A' là trung điểm của AA". Từ đó suy ra \(A"\left(\frac{5}{3};\frac{8}{3};-\frac{1}{3}\right)\)
Đúng 0
Bình luận (0)