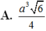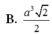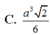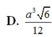Cho hình chóp S.ABC có AB=a, AC=2a, góc B A C ^ = 60 ° , cạnh S A = a 3 và vuông góc với mặt phẳng (ABC). Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
A. a 55 6
B. a 7 2
C. a 10 2
D. a 11 2
Cho hình chóp S.ABC có AB=a, AC=2a, B A C ^ = 60 ° , cạnh bên SA vuông góc với đáy và S A = a 3 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC
A. R = a 7 2
B. R = a 55 6
C. R = a 10 2
D. R = a 11 2
Cho hình chóp S.ABC có đáy là tam giác vuông tại A , A C = a , B C = 2 a . Hình chiếu của S trên ( ABC) là trung điểm H của BC. Cạnh bên SB tạo với đáy một góc 60 ° . Thể tích khối chóp S.ABC là
A. a 3 6
B. a 3 3 12
C. a 3 3 5
D. a 3 2
Đáp án D
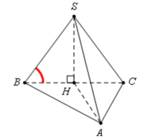
Ta có S H ⊥ A B C ⇒ S B ; A B C ^ = S B ; B C ^ = S B C ^ = 60 °
Tam giác SBH vuông tại H, có S H = tan 60 ° . B H = a 3
Và S A B C = 1 2 . A B . A C = a 2 3 2 .
Vậy thể tích khối chóp là V S . A B C D = 1 3 . S H . S A B C = 1 3 a 3 a 2 3 2 = a 3 2
Cho hình chóp S.ABC có SA vuông góc (ABC) . Cho tam giác ABC vuông B có AB=2a ,BC=a Biết cạnh SB tạo với đáy một góc 60
a) Xác định tâm và bán kính mặt cầu ngoại tiếp S.ABC
b) Tính S mặt cầu và Vkhối cầu
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=a, AB=a, AC=2a. B A C ^ = 60 ∘ . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC.
A. V = 20 5 π a 3 3
B. V = 5 6 π a 3
C. 5 5 π 2 a 3
D. V = 5 5 6 π a 3
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), S A = a , A B = a , A C = 2 a , B A C = 60 ° . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC
A. V = 20 5 π a 3 3
B. V = 5 5 6 π a 3
C. V = 5 5 π 2 a 3
D. V = 5 6 π a 3
Đáp án B
Phương pháp:
- Chứng minh Δ A B C vuông tại B, tìm tâm và bán kính đường tròn ngoại tiếp tam giác đáy.
- Sử dụng công thức R 2 = h 2 4 + r 2 với R là bán kính hình cầu ngoại tiếp khối chóp, h là chiều cao, r là bán kính đường tròn ngoại tiếp đa giác đáy.
Cách giải:
Ta có: cos 60 ° = 1 2 = a 2 a → cos B A C = A B A C
⇒ Δ A B C vuông tại B.
Gọi M là trung điểm AC.
⇒ M là tâm đường tròn ngoại tiếp Δ A B C
⇒ M A = M A = A C 2 = a

Gọi r là bán kính đường tròn ngoại tiếp tam giác đáy.
R là bán kính mặt cầu ngoại tiếp hình chóp.
h là chiều cao hình chóp.
Ta có công thức sau:
R 2 = h 2 4 + r 2 ⇒ R 2 = a 2 4 + a 2 = a 5 2
⇒ V = 4 3 π R 3 = 5 a 5 6
Chú ý khi giải:
HS cần linh hoạt trong việc chứng minh Δ A B C vuông tại B và biết sử dụng công thức liên hệ giữa R, r, h.
cho một hình chóp S.ABC có SA vuông góc (abc) SA=AC=2a, AB=a, gócBAC=60°. Tính thể tích khối chóp
Bố của Nam sinh năm 1980. Năm đó thuộc thế kỉ nào?
Nhanh nhẹn lên.
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A,BC=2a,AC=a/2,SB vuông góc với đáy. Góc giữa cạnh bên SC và mặt đáy bằng 60 độ. Tính theo a thể tích khối chóp S.ABC
A. a 3 5 2
B. a 3 5 4
C. a 3 5 12
D. a 3 5 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và SC = 2a√5 . Hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm M của cạnh AB. Góc giữa đường thẳng SC và (ABC) bằng 600. Tính thể tích khối chóp S.ABC theo a.
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, AB=2a,AC=a và SA vuông góc với mặt phẳng (ABC). Biết góc giữa hai mặt phẳng (SAB) và (SBC) bằng 60°. Tính thể tích khối chóp S.ABC.