Từ đẳng thức 1 t 5 + 4 cos 3 u - 2 sin 2 v + C = ∫ f ( t ) d t có tìm được hàm số y = f(x) hay không ?
![]()
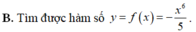
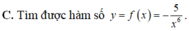
![]()
Bài 5 :
1 ) Cho \(\cos\alpha=\frac{3}{5}va0< \alpha< \frac{\pi}{2}.\) Tìm \(\sin\alpha\) ?
2 ) Chứng minh đẳng thức \(2\sin^6x-3\sin^4x+1=3\cos^4x-2\cos^6x\)
Câu này, mọi người giúp với !!! Mình đã tìm ra được hằng đẳng thức của (Sin3)2 + (Cos3)2 và tương tự nhưng chưa khai triển được
D = 2(Sin6α + Cos6α) - 3(Sin4α + Cos4α)
\(D=2\left(sin^2x+cos^2x\right)\left(sin^4x+cos^4x-sin^2x.cos^2x\right)-3\left(sin^4x+cos^4x\right)\)
\(=2\left(sin^4x+cos^4x\right)-2sin^2x.cos^2x-3\left(sin^4x+cos^4x\right)\)
\(=-\left(sin^4x+2sin^2x.cos^2x+cos^4x\right)\)
\(=-\left(sin^2x+cos^2x\right)^2=-1\)
Chứng minh đẳng thức sau: \(\dfrac{3}{4}-\cos^2\left(a-\dfrac{\pi}{3}\right)+\cos a.\cos\left(a-\dfrac{\pi}{3}\right)=\cos^2a\)
\(VT=\dfrac{3}{4}-\dfrac{1}{2}-\dfrac{1}{2}cos\left(2a-\dfrac{2\pi}{3}\right)+\dfrac{1}{2}cos\left(2a-\dfrac{\pi}{3}\right)+\dfrac{1}{2}cos\left(\dfrac{\pi}{3}\right)\)
\(=\dfrac{1}{2}+\dfrac{1}{2}\left[cos\left(2a-\dfrac{\pi}{3}\right)-cos\left(2a-\dfrac{2\pi}{3}\right)\right]\)
\(=\dfrac{1}{2}-sin\left(2a-\dfrac{\pi}{2}\right)sin\left(\dfrac{\pi}{6}\right)\)
\(=\dfrac{1}{2}+\dfrac{1}{2}cos2a=\dfrac{1}{2}+\dfrac{1}{2}\left(2cos^2a-1\right)=cos^2a\)
Chứng minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa)
a) $\sin ^{4} x+\cos ^{4} x=1-2 \sin ^{2} x \cdot \cos ^{2} x$.
b) $\dfrac{1+\cot x}{1-\cot x}=\dfrac{\tan x+1}{\tan x-1}$.
c) $\dfrac{\cos x+\sin x}{\cos ^{3} x}=\tan ^{3} x+\tan ^{2} x+\tan x+1$.
\(a)sin^4x+cos^4x=1-2sin^2x\cdot cos^2x\)
\(\Leftrightarrow sin^4x+2sin^2x\cdot cos^2x+cos^4x=1\)
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2=1\)(luôn đúng)
a) VT=(sin2x + cos 2 x)2 - 2sin2 x . cos2 x = VP
b) VT= \(\dfrac{1+\dfrac{1}{tanx}}{1-\dfrac{1}{tanx}}\)=VP
c) VT= \(\dfrac{1}{cos^2x}+\dfrac{sinx}{cosx}.\dfrac{1}{cos^2x}=1+tan^2x+tanx.\left(1+tan^2x\right)=VP\)
Chứng minh các đẳng thức:
\(cos^3xsinx-sin^3xcosx=\dfrac{1}{4}sin4x\)
\(sin^4x+cos^4x=\dfrac{1}{4}\left(3+cos4x\right)\)
\(cos^3xsinx-sin^3xcosx=sinx.cosx\left(cos^2x-sin^2x\right)=\dfrac{1}{2}sin2x.cos2x=\dfrac{1}{4}sin4x\)
\(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=1-\dfrac{1}{2}\left(2sinx.cosx\right)^2=1-\dfrac{1}{2}sin^22x\)
\(=1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{1}{4}\left(3+cos4x\right)\)
Chứng minh các đẳng thức lượng giác sau:
a) \({\sin ^4}\alpha - {\cos ^4}\alpha = 1 - 2{\cos ^2}\alpha \)
b) \(\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}\)
a) Ta có:
\(\begin{array}{l}{\sin ^4}\alpha - {\cos ^4}\alpha = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\left( {{{\sin }^2}\alpha - {{\cos }^2}\alpha } \right) = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow {\sin ^2}\alpha - {\cos ^2}\alpha - 1 + 2{\cos ^2}\alpha = 0\\ \Leftrightarrow {\sin ^2}\alpha + {\cos ^2}\alpha - 1 = 0\\ \Leftrightarrow 1 - 1 = 0\\ \Leftrightarrow 0 = 0\end{array}\)
Đẳng thức luôn đúng
b) Ta có:
\(\begin{array}{l}\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{\cos \alpha .\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{1}{{\sin \alpha .\cos \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\end{array}\)
Đẳng thức luôn đúng
Chứng minh đẳng thức:
2\(\left(\sin^6\alpha+\cos^6\alpha\right)+1=3\left(\sin^4\alpha+\cos^4\alpha\right)\)
\(2\left(sin^6x+cos^6x\right)+1=2\left(sin^2x+cos^2x\right)^3-6sin^2x.cos^2x\left(sin^2x+cos^2x\right)+1\)
\(=3-6sin^2x.cos^2x\) (1)
\(3\left(sin^4x+cos^4x\right)=3\left(sin^2x+cos^2x\right)^2-6sin^2x.cos^2x\)
\(=3-6sin^2x.cos^2x\) (2)
(1);(2) \(\Rightarrow\) đpcm
Các đẳng thức sau có thể đồng thời xảy ra không?
a) \(\sin \alpha = \frac{3}{5}\) và \(\cos \alpha = - \frac{4}{5}\)
b) \(\sin \alpha = \frac{1}{3}\) và \(\cot \alpha = \frac{1}{2}\)
c) \(\tan \alpha = 3\) và \(\cot \alpha = \frac{1}{3}\)
a, Ta có: \(sin^2\alpha+cos^2\alpha=1\Leftrightarrow\left(\dfrac{3}{5}\right)^2+cos^2\alpha=1\Leftrightarrow cos\alpha=\pm\dfrac{4}{5}\)
Vậy đẳng thức có thể đồng thời xảy ra.
b, Ta có: \(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\Rightarrow1+cot^2\alpha=\dfrac{1}{\left(\dfrac{1}{3}\right)^2}\Rightarrow cot\alpha=\pm2\sqrt{2}\)
Hai đẳng thức không thể đồng thời xảy ra.
c, Ta có: \(tan\alpha\cdot cot\alpha=1\Rightarrow3\cdot cot\alpha=1\Rightarrow cot\alpha=\dfrac{1}{3}\)
Đẳng thức có thể đồng thời xảy ra.
Cho góc bất kì \(\alpha \). Chứng minh các đẳng thức sau:
a) \({\left( {\sin \alpha + \cos \alpha } \right)^2} = 1 + \sin 2\alpha ;\;\)
b) \({\cos ^4}\alpha - {\sin ^4}\alpha = \cos 2\alpha .\)
a) Ta có: \({\left( {\sin \alpha + \cos \alpha } \right)^2} = {\sin ^2}\alpha + 2\sin \alpha \cos \alpha + {\cos ^2}\alpha = 1 + \sin 2\alpha \;\)
b) \({\cos ^4}\alpha - {\sin ^4}\alpha = \left( {{{\cos }^2}\alpha - {{\sin }^2}\alpha } \right)\left( {{{\cos }^2}\alpha + {{\sin }^2}\alpha } \right) = \cos 2\alpha \;\)
1. Biểu thức A = \(\frac{1}{2\sin10}-2\sin70\) có gái trị bằng bao nhiêu ?
2. Tích số cos10.cos30.cos50.cos70 = ?
3. Tích số \(cos\frac{\pi}{7}.cos\frac{4\pi}{7}.cos\frac{5\pi}{7}\) = ?
4. Tính A = \(\frac{tan30+tan40+tan50+tan60}{cos20}\)=?
5.Rút gọn biểu thức : cos54.cos4 - cos36.cos86
=> P/S : (Làm theo công thức lượng giác lớp 10 ở tất cả các câu)
Câu 3:
\(A=cos\frac{\pi}{7}.cos\frac{5\pi}{7}.cos\frac{4\pi}{7}=cos\frac{\pi}{7}.cos\left(\pi-\frac{2\pi}{7}\right).cos\frac{4\pi}{7}\)
\(A=-cos\frac{\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(\Rightarrow sin\frac{\pi}{7}.A=-\frac{1}{2}.2sin\frac{\pi}{7}.cos\frac{\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(\Rightarrow sin\frac{\pi}{7}.A=-\frac{1}{2}.sin\frac{2\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(\Rightarrow sin\frac{\pi}{7}.A=-\frac{1}{4}sin\frac{4\pi}{7}.cos\frac{4\pi}{7}\)
\(\Rightarrow sin\frac{\pi}{7}.A=-\frac{1}{8}sin\frac{8\pi}{7}=-\frac{1}{8}sin\left(\pi+\frac{\pi}{7}\right)=\frac{1}{8}sin\frac{\pi}{7}\)
\(\Rightarrow A=\frac{1}{8}\)
Câu 4:
Đầu tiên ta chứng minh công thức:
\(tana+tanb=\frac{sina}{cosa}+\frac{sinb}{cosb}=\frac{sina.cosb+cosa.sinb}{cosa.cosb}=\frac{sin\left(a+b\right)}{cosa.cosb}\)
Áp dụng để biến đổi tử số:
\(tan30+tan60+tan40+tan50=\frac{sin90}{cos30.cos60}+\frac{sin90}{cos40.cos50}=\frac{1}{cos30.cos60}+\frac{1}{cos40.cos50}\)
\(=\frac{2}{cos90+cos30}+\frac{2}{cos90+cos10}=\frac{2}{cos30}+\frac{2}{cos10}=2\left(\frac{cos30+cos10}{cos30.cos10}\right)\)
\(=2\left(\frac{2cos20.cos10}{cos30.cos10}\right)=\frac{4.cos20}{cos30}=\frac{8\sqrt{3}}{3}.cos20\)
\(\Rightarrow A=\frac{\frac{8\sqrt{3}}{3}cos20}{cos20}=\frac{8\sqrt{3}}{3}\)
Câu 5:
\(cos54.cos4-cos36.cos86=cos54.cos4-cos\left(90-54\right).cos\left(90-4\right)\)
\(=cos54.cos4-sin54.sin4=cos\left(54+4\right)=cos58\)
Câu 1:
\(A=\frac{1}{2sin10}-2sin70=\frac{1-4sin10.sin70}{2sin10}=\frac{1+2\left(cos80-cos60\right)}{2sin10}\)
\(=\frac{1+2cos80-1}{2sin10}=\frac{2cos80}{2sin10}=\frac{sin10}{sin10}=1\)
Câu 2:
\(cos10.cos30.cos50.cos70=cos10.cos30.\frac{1}{2}\left(cos120+cos20\right)\)
\(=\frac{1}{2}cos30\left(cos10.cos120+cos10.cos20\right)\)
\(=\frac{1}{2}cos30\left(cos10.cos120+\frac{1}{2}\left(cos30+cos10\right)\right)\)
\(=\frac{1}{2}cos30\left(cos10.cos120+\frac{1}{2}cos30+\frac{1}{2}cos10\right)\)
\(=\frac{1}{2}.\frac{\sqrt{3}}{2}\left(-\frac{1}{2}cos10+\frac{1}{2}\frac{\sqrt{3}}{2}+\frac{1}{2}cos10\right)\)
\(=\frac{3}{16}\)