Cho dãy số u n = − 2 n . chọn khẳng định đúng trong các khẳng định sau?
A. Dãy số u n không bị chặn
B. Dãy số u n bị chặn.
C. Dãy số tăng
D. Dãy số giảm.
Cho dãy số u n = − 2 n . chọn khẳng định đúng trong các khẳng định sau?
A. Dãy số u n không bị chặn.
B. Dãy số u n bị chặn.
C. Dãy số tăng.
D. Dãy số giảm.
Cho dãy số ( u n ) với u n = − 1 n sin π n , chọn khẳng định đúng trong các khẳng định sau?
A. Dãy số ( u n ) là dãy số tăng
B. Dãy ( u n ) bị chặn dưới nhưng không bị chặn trên
C. Dãy số ( u n ) bị chặn
D. Dãy số ( u n ) bị chặn trên nhưng không bị chặn dưới
Đáp án C
Ta có u n = − 1 n sin π n = sin π n ≤ 1
⇒ Dãy số ( u n ) bị chặn
Chọn khẳng định đúng trong các khẳng định sau: A.2/3 € Q B. -2/9 € N C.-6 € N D. -3/5 € Z
Cho ∫ 0 1 x 2 3 x 3 + 4 d x và u = 3 x 3 + 4 . Chọn khẳng định đúng trong các khẳng định sau:
A. 2 9 ∫ 2 7 u 2 d u
B. 1 3 ∫ 2 7 u 2 d u
C. 1 9 ∫ 2 7 u 2 d u
D. 2 9 ∫ 0 1 u 2 d u
Cho ∫ 0 1 x 2 3 x 3 + 4 d x và u = 3 x 3 + 4 . Chọn khẳng định đúng trong các khẳng định sau:
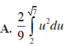
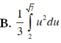
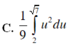
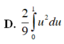
Cho hàm số y = x 4 − 3 x 2 + 2 .Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số có 2 cực đại và 1 cực tiểu.
B. Hàm số có đúng một điểm cực trị.
C. Hàm số luôn đồng biến trên R.
D. Hàm số có 2 cực tiểu và 1 cực đại.
Đáp án B
Hàm số y = x 4 − 3 x 2 + 2 có a,b trái dấu và a>0 nên hàm số có 2 cực tiểu và 1 cực đại.
Cho dãy số ( x n ) : x 0 = 1 x n = 2 n ( n - 1 ) 2 ∑ i = 1 n - 1 x i , n = 2 , 3 . . . . . Xét dãy số yn = xn+1 - xn. Khẳng định nào đúng về dãy (yn)
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn A.
Ta có: 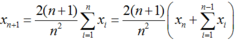
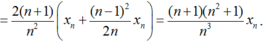
Do đó: 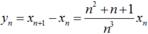
- Ta chứng minh dãy (yn) tăng.
Ta có: 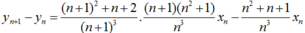
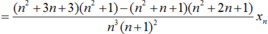
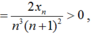
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
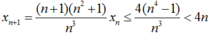
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: 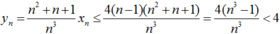
Vậy bài toán được chứng minh.
Cho dãy số (un) có un = 1/n+2 với n thuộc N*. Khẳng định nào sau đây là đúng?
Xét `H=u_[n+1]-u_n`
`=1/[n+3]-1/[n+2]`
`=[n+2-n-3]/[(n+3)(n+2)]=[-1]/[(n+3)(n+2)]`
Với `n in NN`*`=>(n+3)(n+2) > 0<=>[-1]/(n+3)(n+2)] > 0`
`=>H > 0`
`->\bb D`
Chọn B, do mọi số hạng của dãy số này đều lớn hơn 0.
Cho hàm số f x = 2 x 2 x . Chọn khẳng định đúng trong các khẳng định sau
A. Vì lim x → 0 + f x = lim x → 0 − f x nên f( x)liên tục tại x = 0
B. Hàm số f (x )xác định với mọi x ≠ 0.
C. lim x → 0 + f x ≠ lim x → 0 − f x
D. Hàm số f ( x) liên tục trên ℝ
Đáp án B
Hàm số f ( x) xác định với mọi x ≠ 0.