Cho cấp số cộng ( u n ) biết u 5 = 18 v à 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 2 , d = 4
B. u 1 = 2 , d = 3
C. u 1 = 2 , d = 2
D. u 1 = 3 , d = 2
Cho cấp số cộng (un) có u4=-12, u14=18. Tính tổng 16 số hạng đầu tiên cua cấp số cộng này
\(\left\{{}\begin{matrix}u_{14}=u_1+13d=18\\u_4=u_1+3d=-12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}d=3\\u_1=-21\end{matrix}\right.\)
Tổng 16 số hạng đầu tiên:
\(S_{16}=\frac{16\left(2u_1+15d\right)}{2}=24\)
Cho cấp số cộng (un) biết \(\left\{{}\begin{matrix}u_3=5\\S_8=48\end{matrix}\right.\) . Tìm số hạng đầu tiên và tổng 20 số hạng đầu của cấp số công đã cho.
cho (Un) là cấp số cộng U3 +U13=80 .tổng 15 số hạng đầu tiên của cấp số cộng đố bằng bao nhiêu
tìm n nguyên đểcác biểu thức sau à số nguyên :
A bằng 2n -5
n cộng 1
A nguyên khi :
2n - 5 ⋮ n + 1
=> 2n + 2 - 7 ⋮ n + 1
=> 2(n + 1) - 7 ⋮ n + 1
=> 7 ⋮ n + 1
=> n + 1 thuộc Ư(7)
=> n + 1 thuộc {-1; 1; -7; 7}
=> n thuộc {-2; 0; -8; 6}
vậy_
Ta có : \(A\inℤ\Leftrightarrow2n-5⋮n+1\)
\(\Rightarrow2n+2-7⋮n+1\)
\(\Rightarrow2\left(n+1\right)-7⋮n+1\)
mà \(2\left(n+1\right)⋮n+1\)
\(\Rightarrow-7⋮n+1\)
\(\Rightarrow n+1\inƯ\left(-7\right)\)
\(\Rightarrow n+1\in\left\{1;7;-1;-7\right\}\)
Lập bảng xét 4 trường hợp :
| \(n+1\) | \(1\) | \(7\) | \(-1\) | \(-7\) |
| \(n\) | \(0\) | \(6\) | \(-2\) | \(-8\) |
Vậy \(n\in\left\{0;6;-2;-8\right\}\)
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Cho dãy (un) là cấp số cộng vs công sai d khác 0 vậy dãy (5nu) là dãy gì? (Cấp số cộng hay nhân và công bội hay công sai là bao nhiêu hay đều k phải cấp số nhân và cộng)
Giúp mình vs mình đang cần gấp!!!
Ý bạn là dãy \(5u_n\)
Đặt \(u_n=u_1+\left(n-1\right)d\)
\(v_n=5u_n=5u_1+\left(n-1\right).5d\)
Vậy dãy mới là 1 cấp số cộng với số hạng đầu bằng \(u_1'=5u_1\) và công sai \(d'=5d\)
Cho cấp số cộng (Un) với u3+u5=5 và u3×u5=6 tìm số hạng đầu của cấp số cộng và cấp số nhân
Gọi số hạng đầu và công sai lần lượt là \(u_1\) và \(d\)
\(\left\{{}\begin{matrix}u_3+u_5=5\\u_3u_5=6\end{matrix}\right.\)
Theo định lý Viet đảo, \(u_3\) và \(u_5\) là nghiệm của pt:
\(x^2-5x+6=0\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}u_3=2\\u_5=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1+2d=2\\u_1+4d=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=\frac{1}{2}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}u_3=3\\u_5=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1+2d=3\\u_1+4d=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=4\\d=-\frac{1}{2}\end{matrix}\right.\)
Cho cấp số cộng u n biết u 5 = 18 v à 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 2 ; d = 4
B. u 1 = 2 ; d = 3
C. u 1 = 2 ; d = 2
D. u 1 = 3 ; d = 2
Chọn đáp án A
Ta có: u 5 = 18 ⇔ u 1 + 4 d = 18 ( 1 )
Với n = 5 n ê n 4 S 5 = S 10
⇔ 2 u 1 - d = 0
Khi đó ta có hệ phương trình
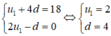
cho số N nguyên dương và dãy A gồm N phần tử kiểm tra xem dãy số vừa nhập có phải là một cấp số cộng hay không
VD: N= 4
Dãy A: 1 2 3 4 à là cấp số cộng với công sai d=1
Yêu cầu:
- xác định bài toán
- nêu ý tưởng
- mô tả thuật toán
Input: dãy A và N phần tử
Output: Là cấp số cộng hoặc không là cấp số cộng
Thuật toán:
- Bước 1: Nhập N và dãy A1,A2,...,An
- Bước 2: d←A2-A1; i←2;
-Bước 3: Nếu i>N thì in ra kết quả là cấp số cộng rồi kết thúc
- Bước 4: Nếu Ai+1-Ai khác d thì chuyền xuống bước 6
- Bước 5: i←i+1, quay lại bước 3
- Bước 6: Thông báo không phải là cấp số cộng rồi kết thúc
Cho cấp số cộng ( u n ) biết u 5 = 18 và 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 3 ; d = 2
B. u 1 = 2 ; d = 3
C. u 1 = 2 ; d = 2
D. u 1 = 2 ; d = 4
Đáp án D
u 5 = 18 ⇔ u 1 + 4 d = 18 ( 1 )
4 S n = S 2 n
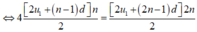
⇒ 2 u 1 - d = 0 ( 2 )
Từ (1) & (2) ta có u 1 = 2 ; d = 2