1/

 

Kẻ AH \(\perp\)CD , \(BK\perp CD\)

Xét tam giác vuông AHD và tam giác vuông BKC, có: góc ADH = góc BCK = 60⁰ ; cạnh AH = BK

   => tam giác AHD = tam giác BKC (gcg) 

   => DH = KC 

Đặt a = DH (a > 0) => AH = \(\sqrt{1-x^2}\)

Có: Sin60 = \(\frac{AH}{AD}\Rightarrow\frac{\sqrt{3}}{2}=\sqrt{1-x^2}\Rightarrow1-x^2=\frac{3}{4}\Rightarrow x^2=\frac{1}{4}\Rightarrow\left[\begin{array}{nghiempt}x=\frac{1}{2}\left(n\right)\\x=-\frac{1}{2}\left(l\right)\end{array}\right.\)

    => x = 1/2 hay DH = KC = 1/2 

Mặt khác: HK = CD - (DH + KC) = 2,7 - (1/2 + 1/2) = 1,7 (m)

Tứ giác ABCD là hình chữ nhật (góc AHK = góc BKH = ABK = 90⁰) => AB = HK = 1,7 (m)

    Vậy AB = 1,7m

2/ 

a/ Cm: tam giác ICD đều:

 Trong tam giác ICD : DB vừa là đường phân giác , vừa là đường cao => tam giác ICD là tam giác cân tại D 

 => ID = DC (1)

 => DB vừa là đường trung tuyến => BI = BC = 4cm => IC = 4 + 4 = 8cm (2)

 Có: góc IAB = IDC (đồng vị) , góc IBA = góc ICD (đồng vị) 

       mà góc IDC = góc ICD

    => góc IAB = góc IBA => tam giác IAB cân tại I => IA = IB = 4cm

    => ID = IA + AD = 4 + 4 = 8cm (3) 

 Từ (1), (2), (3) => ID = DC = IC = 8cm hay tam giác IDC đều

b/ Tính chu vi hình thang ABCD:

 Vì tam giác ICD đều => tam giác IAB đều => IA = AB = 4cm

 ID = DC = 8cm

 Vậy chu vi hình thang ABCD : AB + AD + BC + CD = 4 + 4 + 4 + 8 = 20(cm)

a

2 góc A, B bằng 120 độ

2 góc C, D bằng 60 độ

chứng minh 90 độ - góc BCA = 0 suy ra góc BCA = 30 độ

b) chỉ cân chứng minh AD = 1/2 BC

trong tam giác ACD vuông có 1 góc 30 độ, 1 góc 60 độ

nên góc đối diện với góc 30 độ bằng 1/2 cạnh huyền

Đáp án D

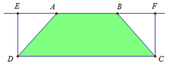
Ta có:  A E = B F = 1

Khi đó:  D E = A D 2 − A E 2 = 1

Khi quay hình chữ nhật DEFC quanh trục AB ta được hình trụ có thể tích là:

V 1 = π D E 2 . D C = π .1 2 .3 = 3 π

Khi quay tam giác AED quanh trục AB ta được hình nón có thể tích là:

V 2 = 1 3 π D E 2 . A E = 1 3 π .1 2 .1 = π 3

Do đó thể tích vận tròn xoay tạo thành khi cho hình thang quay quanh AB là:

V = V 1 − 2 V 2 = 7 π 3

Chọn đáp án D